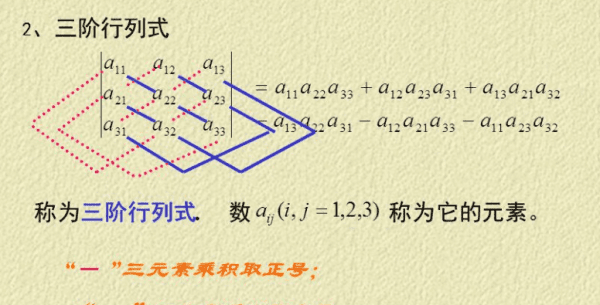
什么是对角行列式
对角行列式是三角形行列式的特例,就是除主对角线上的元素外其余元素为0,它的值是主对角线上的n个元素之积“1”,而且值的符号是由主对角线上n个元素之积的符号确定。
对角是指在三角形中两边所夹的内角称为第三边的对角,而且对角的应用有等角对等边,三角形中如果两个内角相等,则它们的对边也相等,故可以根据三角形内角是否相等判断它是否为等腰三角形。
三对角行列式是什么意思
三对角行列式是:一个三对角矩阵的非零系数在如下的三条对角线上:主对角线、低对角线、高对角线。
在许多物理问题中,三对角矩阵常常作为原始数据出现,因此它们本身是很重要的,这种矩阵仅有(2n-1)个独立的元素。
在线性代数中,三对角矩阵是矩阵的一种,它“几乎”是一个对角矩阵。由三对角矩阵确定特征值由一些较有效的方法,常见的有两种:QR法、特征多项式法。由两个三元一次方程所组成的方程组来表示。含有n个未知量的一次方程称为线性方程。关于变量是一次的函数称为线性函数。

相关信息
线性代数在数学、物理学和技术学科中有各种重要应用,因而它在各种代数分支中占居首要地位。在计算机广泛应用的今天,计算机图形学、计算机辅助设计、密码学、虚拟现实等技术无不以线性代数为其理论和算法基础的一部分。
线性代数所体现的几何观念与代数方法之间的联系,从具体概念抽象出来的公理化方法以及严谨的逻辑推证、巧妙的归纳综合等,对于强化人们的数学训练,增益科学智能是非常有用的。随着科学的发展,我们不仅要研究单个变量之间的关系。
还要进一步研究多个变量之间的关系,各种实际问题在大多数情况下可以线性化,而由于计算机的发展,线性化了的问题又可以被计算出来,线性代数正是解决这些问题的有力工具。线性代数的计算方法也是计算数学里一个很重要的内容。
三对角行列式是什么意思
三对角行列式:一个三对角矩阵的非零系数在主对角线上,或比主对角线低一行的对角线上,或比主对角线高一行的对角线上。
形如这样的矩阵就叫三对角行列式:
WBR|* WBR * WBR 0 WBR WBR 0 WBR WBR 0 | WBR
WBR |* WBR * WBR * WBR 0 WBR WBR 0 | WBR
WBR |0 WBR * WBR * WBR * WBR 0 | WBR
WBR |0 WBR WBR 0 WBR * WBR * WBR * | WBRWBR
WBR |0 WBR WBR 0 WBR WBR 0 WBR * WBR * | WBR
副下三角行列式定义及计算公式
三角形行列式的计算公式是D=|A|=detA=det(aij),定义是在计算行列式(特别是数字行列式)时,可先利用行列式的性质,把行列式化为上(下)三角形行列式,再利用上面的结果进行计算。副对角行列式的计算公式是D=|A|=detA=det。定义是副对角行列式指的不是第一行和最后一行交换,而是最后一行依次和其他行交换到第一行去。
第n行和第n-1行交换,它变成了第n-1行,再和第n-2行交换,这样一直到最后和第一行交换。共进行了n-1次交换。总共要交换 1+2+3+...+n-1=(1+n-1)(n-1)/2=n(n-1)/2次。
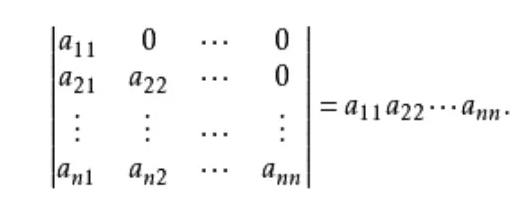
化为上(下)三角形行列式:
1、行列式所有行(或列)全部元素化为1;
2、对爪形(三线型)行列式,可通过将其余各行(或列)的某一倍数加到第1行(或列)而化为三角形行列式;
3、若行列式的各行(或列)之间差别不大,可采用逐行(或列)相加(或减)的方法,将其化简后进行计算;
4、对某些行列式,可在原行列式中增加一行一列,且保持原行列式不变,使其具有某种特征,便于计算,一般称此法为加边法。
以上就是关于什么是对角行列式,三对角行列式是什么意思的全部内容,以及什么是对角行列式的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。