矩阵是数表吗?
矩阵是数表。
矩阵的定义为:由m×n个数aij排成的m行n列的数表称为m行n列的矩阵,简称m×n矩阵。
这m×n个数称为矩阵A的元素,简称为元,数aij位于矩阵A的第i行第j列,称为矩阵A的(i,j)元,以数aij为(i,j)元的矩阵可记为(aij)或(aij)m×n,m×n矩阵A也记作Amn。
由定义可得矩阵是数表。
矩阵和行列式的区别及联系
一、矩阵和行列式的区别:
1、数学中定义不同
行列式在数学中,是一个函数,其定义域为det的矩阵A,取值为一个标量,写作det(A)或|A|。
在数学中,矩阵是一个按照长方阵列排列的复数或实数集合,最早来自于方程组的系数及常数所构成的方阵。

2、应用范围不同
行列式无论是在线性代数、多项式理论,还是在微积分学中(比如说换元积分法中),行列式作为基本的数学工具,都有着重要的应用。
矩阵在物理学中,矩阵于电路学、力学、光学和量子物理中都有应用,计算机科学中,三维动画制作也需要用到矩阵。
二、矩阵和行列式的联系:
行列式是一个数值,矩阵是一个数表,行列式可看作一个n行n列矩阵(即方阵)的行列式。
扩展资料:
矩阵是高等代数学中的常见工具,也常见于统计分析等应用数学学科中。在物理学中,矩阵于电路学、力学、光学和量子物理中都有应用;计算机科学中,三维动画制作也需要用到矩阵。
矩阵的运算是数值分析领域的重要问题。将矩阵分解为简单矩阵的组合可以在理论和实际应用上简化矩阵的运算。对一些应用广泛而形式特殊的矩阵,例如稀疏矩阵和准对角矩阵,有特定的快速运算算法。在天体物理、量子力学等领域,也会出现无穷维的矩阵,是矩阵的一种推广。
数值分析的主要分支致力于开发矩阵计算的有效算法,这是一个几个世纪以来的课题,是一个不断扩大的研究领域。
矩阵分解方法简化了理论和实际的计算。 针对特定矩阵结构(如稀疏矩阵和近角矩阵)定制的算法在有限元方法和其他计算中加快了计算。
无限矩阵发生在行星理论和原子理论中。 无限矩阵的一个简单例子是代表一个函数的泰勒级数的导数算子的矩阵
参考资料:
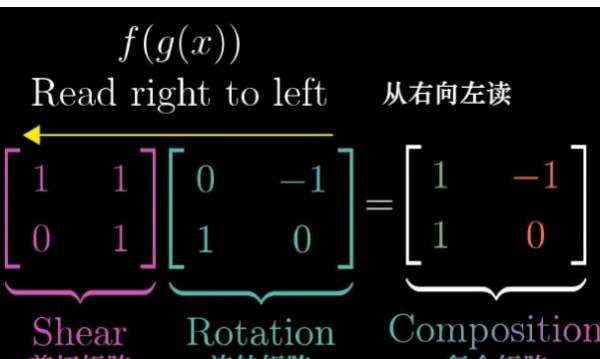
矩阵到底是什么
表示方式不同。矩阵用的是方括号,行列式用的是双垂线,例如[A]这样的就是矩阵,而|A|这样的就是行列式。
形状不同。矩阵的行数和列数可以相等,也可以不等,也就是说矩阵的形状可以是正方形的也可以是长方形的,而行列式的行和列必须相等,其形状必须是正方形的。
意义不同。矩阵在线性代数中的地位和数在初等数学中的地位是一样的,可以进行一些特殊的运算,而行列式则不同,它是有值的,它的值就是一个常数,可以根据其值的定义求出它的值,所以,行列式可以被当作常数来看待,而矩阵不可以。
矩阵是一个数表,分为同型矩阵,系数矩阵等等;行列式就是是一个数。它们各自的加减乘除运算方法不一样。
5.矩阵经初等变换,其秩不变;行列式经初等变换,其值可能改变:换法变换要变号,倍法变换差倍数;消法变换不改变。
矩阵是数表
矩阵就是一个数表,一个矩阵中有m行n列,就表示有mxn个数按固定的位置排列成数表,称其为mxn矩阵,每个数称为元素,如果m=n则称为方阵,m=1可李滑空称为行向量,n=1可称为列向量如果两个矩阵行数和列数都相等,则称为同型矩阵,两个同型矩阵可定义加减法,结果就是两矩阵每个对应位置的元素相加减得到的矩阵,一个矩阵还可以数乘,一个矩阵乘哪瞎以一个数结果是每一让正个元素都乘以这个数得到的矩阵矩阵就代表一个看做一个整体的表,你在具体问题中赋予它什么意义他就代表什么意义[tele.str3.cn/article/519467.html]
[tele.dcgscs.cn/article/817254.html]
[tele.mdybag.cn/article/345189.html]
[tele.51heycar.cn/article/819760.html]
[tele.sxhthb.cn/article/470982.html]
[tele.jchdmc.cn/article/839542.html]
[tele.sxhthb.cn/article/538710.html]
[tele.jchdmc.cn/article/695342.html]
[tele.jydhy.cn/article/853126.html]
[tele.mayeeage.cn/article/729416.html]
以上就是关于矩阵是数表,矩阵和行列式的区别及联系的全部内容,以及矩阵是数表吗?的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。






