圆锥的外接球半径怎么求
(h-R)?+r?=R?(圆锥的高为h,圆锥底面半径为r,圆锥外接球半径为R),已知两个变量,可求出半径。
圆锥是一种几何图形,有两种定义。解析几何定义是圆锥面和一个截它的平面(满足交线为圆)组成的空间几何图形叫圆锥。立体几何定义是以直角三角形的直角边所在直线为旋转轴,其余两边旋转360度而成的曲面所围成的几何体叫做圆锥。
立体几何的圆锥的外接球的半径怎么求
首先将底面放在立体几何的xy平面上,然后用已知条件表示出四个顶点的坐标,之后通过圆的方程解出底面外心的为位置,然后连接外心和顶点,再用球心到四个顶点距离相等(到顶点和另一个底面上的顶点距离相等即可),从而求出外接球球心,然后就很容易得到半径。
设其棱长为a 则外接球半径R:√6a/4 。
将球心投影到一个面上,且投影是这个三角形的外心,求出三角形外接圆半径r(正余弦定理), 再求球心到这个面的距离d 有勾股定理R²=d²+r²。
外接球八大模型及公式总结图片
类型一:墙角模型(三条线两两垂直)
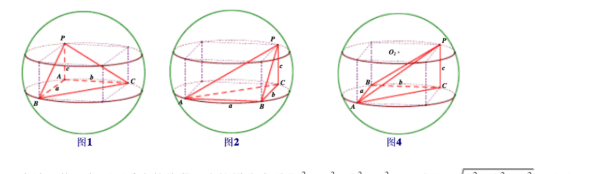
类型二:垂面模型(一条直线垂直于一个平面)

类型三:切瓜模型(两个平面互相垂直)
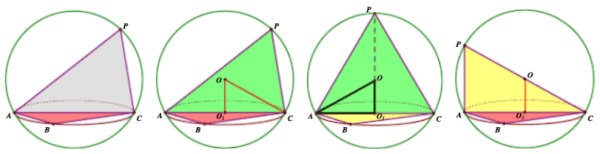
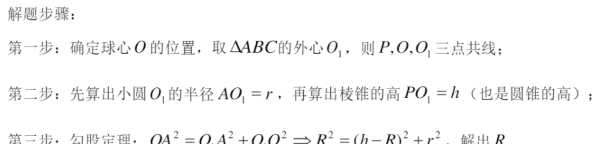
类型四:汉堡模型(直棱柱的外接球)
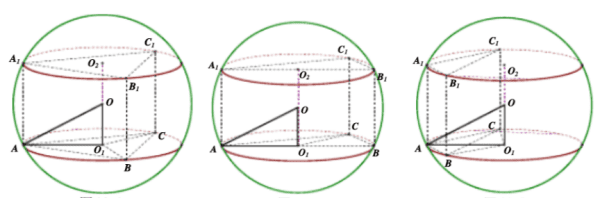
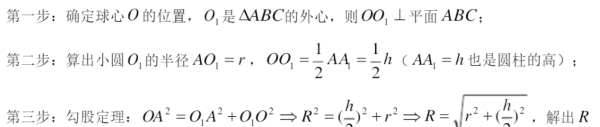
类型五:折叠模型
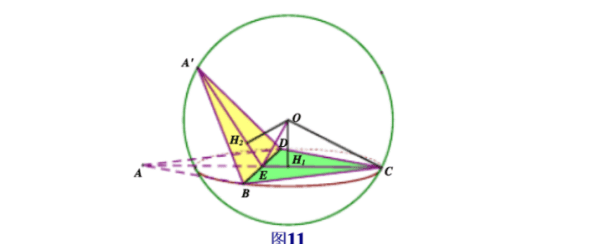

类型六:对棱相等模型
类型七:两直角三角形拼在一起模型
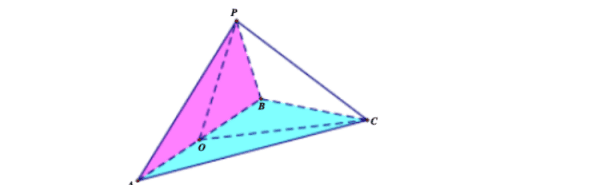

类型八:椎体的内切球问题



外接球半径万能公式:
球体体积=4π/3*(d/2)3
解析:
长方体的空间对角线为外接球的直径,所以先求长方体的空间对角线=﹙a²+b²+c²﹚。
知道直径,然后除以2,得到半径。
再根据球的体积公式求得体积。
1、点O是通过多面体非平行平面外接圆的圆心并垂直于非平行平面的两条直线的交点;
2、点O是通过多面体非平行棱中点、并垂直于这些棱的三个平面的交点;
3、点O是通过一个面的外接圆圆心,且垂直于此圆的平面∑的直线和垂直于过不与∑平行的棱的中点的平面,且垂直于此棱的直线的交点。
已知圆锥的底面半径为2cm,高为2cm,求这个圆锥的体积

圆锥外接球的半径为:(r^2+h^2)/2h
球的体积公式为:4/3πr^3
答案为:32π/3
圆锥外接球半径万能公式
计算圆锥内接球半径的公式为r=2S/(a+B+C)。从球体中心到几何体每个面的距离等于半径的球体是几何体的内接球体。如果一个球与简单多面体或其延伸的每个面相切,并且该球位于多面体内部,则该球称为多面体的内接球。
以上就是关于圆锥的外接球半径怎么,立体几何的圆锥的外接球的半径怎么求的全部内容,以及圆锥的外接球半径怎么求的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。



