怎么证明向量平行
方向相同或相反的非零向量叫做平行向量,平行向量也叫共线向量,非零向量与平行的充要条件是有且只有一个实数λ,向量平行的坐标表示,设a=(x1,y1),b=(x2,y2).其中b≠0,a‖b的充要条件是存在一个实数λ,使a=λ·b。
平行向量,也叫共线向量。是指方向相同或相反的非零向量。零向量与任意向量平行。
向量:既有大小又有方向的量叫向量。
零向量:长度为0的向量,记作→0。
单位向量:长度为1个单位长度的向量。
平行向量:也叫共线向量,方向相同或相反的非零向量。
相等向量:长度相等且方向相同的向量。
相反向量:长度相等且方向相反的向量。
如何证明向量平行
证明向量平行 方法一 证明向量a是向量b的入倍,则向量a平行于b 方法二 两向量对应坐标成比例,则二者平行。
怎么证明两个向量平行大学
方向相同或相反的非零向量叫做平行向量,平行向量也叫共线向量.
非零向量 与 平行的充要条件是有且只有一个实数λ
向量平行的坐标表示
设 a=(x1,y1),b=(x2,y2).其中 b≠0,
a‖ b的充要条件是存在一个实数λ,使
a=λ .b
x1y2-x2y1=0
向量平行公式推导过程
令α=(x1,y1) β=(x2,y2)
则(x1,y1)=λ(x2,y2)
所以x1=λx2,y1=λy2
所以λ=x1/x2=y1/y2
所以x1y2=x2y1
相等的向量一定平行,但是平行的向量并不一定相等。两个向量相等并不一定这两个向量一定要重合。只用这两个向量长度相等且方向相同即可。其中“方向相同”就包含着向量平行的含义。
扩展资料
向量的数量积与实数运算的主要不同点
1.向量的数量积不满足结合律,即:(a·b)·c≠a·(b·c);例如:(a·b)2≠a2·b2。
2.向量的数量积不满足消去律,即:由a·b=a·c(a≠0),推不出b=c。
3.|a·b|与|a|·|b|不等价
4.由 |a|=|b| ,不能推出a=b,也不能推出a=-b,但反过来则成立。
如何证明两向量平行的公式
向量平行公式坐标公式:a=λb,其中b不是零向量。坐标表示:a=(x1,y1),b=(x2,y2),a//b当且仅当x1y2-x2y1=0。
在数学中,向量(也称为欧几里得向量、几何向量、矢量),指具有大小和方向的量。可以形象化地表示为带箭头的线段。箭头所指:代表向量的方向;线段长度:代表向量的大小。与向量对应的只有大小,没有方向的量叫做数量(物理学中称标量)。
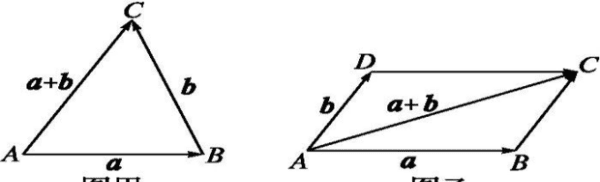
相关信息:
如果e1和e2是同一平面内的两个不共线的非零向量,那么对该平面内的任一向量a,有且只有一对实数λ、μ,使a= λe1+ μe2。
给定空间三向量a、b、c,向量a、b的向量积a×b,再和向量c作数量积(a×b)·c,所得的数叫做三向量a、b、c的混合积,记作(a,b,c)或(abc),即(abc)=(a,b,c)=(a×b)c。
混合积具有下列性质:
1、三个不共面向量a、b、c的混合积的绝对值等于以a、b、c为棱的平行六面体的体积V,并且当a、b、c构成右手系时混合积是正数;当a、b、c构成左手系时,混合积是负数,即(abc)=εV(当a、b、c构成右手系时ε=1;当a、b、c构成左手系时ε=-1)。
2、上条性质的推论:三向量a、b、c共面的充要条件是(abc)=0。
3、(abc) = (bca) = (cab) = - (bac) = - (cba) = - (acb)。
以上就是关于怎么证明向量平行,如何证明向量平行的全部内容,以及怎么证明向量平行的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。