幂的乘方法则的逆用公式
幂的乘方法则的逆用公式:同底数幂的乘法法则为:am·an=am+n(m,n为正整数),将其逆用为am+n=am·an(m,n为正整数)。
同底数幂的乘法法则为:am·an=am+n(m,n为正整数),将其逆用为am+n=am·an(m,n为正整数)。
求n个相同因数乘积的运算,叫做乘方
初一幂的运算所有公式
幂的运算六个基本公式是如下:
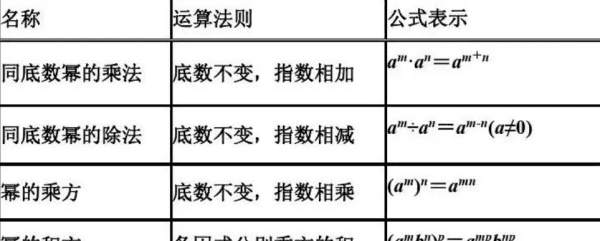
同底数幂相乘a^m·a^n=a^(m+n),幂的乘方(a^m)n=a^mn,积的乘方(ab)^m=a^m·b^m,同底数幂相除a^m÷a^n=a^(m-n)(a≠0),a^(m+n)=a^m·a^n、a^mn=(a^m)·n
同底数幂相乘的性质:
同底数幂相乘,底数不变,指数相加。同底数幂相除,底数不变,指数相减。幂的乘方,底数不变,指数相乘。
同底数幂的除法是整式除法的基础,要熟练掌握。同底数幂的除法法则是根据除法是乘法的逆运算归纳总结出来的,和前面讲的幂的运算的三个法则相比,在这里底数a是不能为零的,否则除数为零,除法就没有意义了。又因为在这里没有引入负指数和零指数,所以又规定m>n。能从特殊到一般地归纳出同底数幂的除法法则。

通过幂的运算到多项式乘法的学习,初步理解“特殊—一般—特殊”的认识规律,发展思维能力。在学习幂的运算性质、乘法法则的过程中,培养观察、综合、类比、归纳、抽象、概括等思维能力。
什么是平方运算的逆运算?
幂运算的逆运算是对数运算
对数的概念:
如果b^n=x,则记n=log(b)(x)。其中,b叫做“底数”,x叫做“真数”,n叫做“以b为底的x的对数”。
关于对数运算在这里有
同底数幂的乘法逆用典型题
同底数幂的乘法逆运算:a的(m+n)次方=a的m次方×a的n次方
积的乘方:
已知(x的3次方)的5次方=-a的15次方b的15次方,则x=
幂的乘方:
已知10的a次方等于5,10的b次方等于6求10的2a+3b次方的值
同底数幂的乘方:
已知n为正整数,试计算(-a)的2n加1次方乘(-a)的3n家2乘(-a)
同底数幂的乘法
法则是本章中的第一个幂的运算法则,也是整式乘法的主要依据之一。学习这个法则时应注意以下五个问题:
(1)先弄清楚底数、指数、幂这三个基本概念的涵义。
(2)它的前提是“同底”,而且底可以是一个具体的数或字母,也可以是一个单项式或多项式,如:
(2x+y)2·(2x+y)3=(2x+y)5,底数就是一个二项式(2x+y)。
幂的四种运算法则和公式
【知识点梳理】
1、同底数幂的乘法:
⑴语言叙述:同底数幂相乘,底数不变,指数相加;
⑵字母表示:am·an= am+n;(m,n都是整数) ;
⑶逆运用:am+n = am·an
2、幂的乘方:
⑴语言叙述:幂的乘方,底数不变,指数相乘;
⑵字母表示:(am) n= amn;(m,n都是整数);
⑶逆运用:amn =(am)n =(an)m;
3、积的乘方:
⑴语言叙述:积的乘方,等于每个因式乘方的积;
⑵字母表示:(ab)n= an bn;(n是整数);
⑶逆运用:an bn = (a b)n;
4、同底数幂的除法:
⑴语言叙述:同底数幂相除,底数不变,指数相减;
⑵字母表示:am÷an= am-n;(a≠0,m、n都是整数);
⑶逆运用:am-n = am÷an
不是确定以及肯定的答案,不喜勿喷O(∩_∩)O
以上就是关于初一幂的运算所有公式,幂的乘方法则的逆用公式的全部内容,以及幂的乘方法则的逆用公式的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。