角的大小与所画角的什么有关
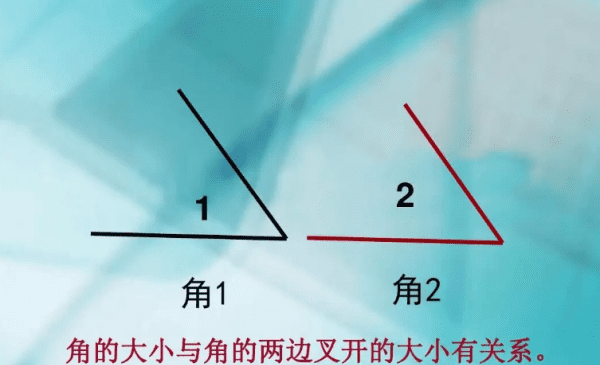
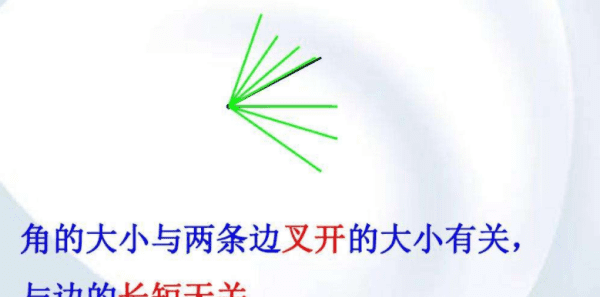
角的大小与所画出的边的长短无关,与两边叉开的大小有关,两边叉开的越大,角越大。
角在几何学中,是由两条有公共端点的射线组成的几何对象,是一条射线绕着它的端点从一个位置旋转到另一个位置所形成的图形。所旋转射线的端点叫做角的顶点,开始位置的射线叫做角的始边,终止位置的射线叫做角的终边。
角的大小是由什么决定的,我的探究方法是
角的大小是由什么决定的答案是:角的两条边张开的程度决定的。
角的大小是由角的两条边张开的程度决定的,张开的越大,角就越大,相反,张开的越小,角则越小。角的大小与角的两条边张开的程度有关,与边的长短无关。
角可以分为锐角、直角、钝角、平角、周角、负角、正角、优角、劣角、0角这10种。以度、分、秒为单位的角的度量制称为角度制。此外,还有密位制、弧度制等。
角在几何学中,是由两条有公共端点的射线组成的几何对象。这两条射线叫做角的边,它们的公共端点叫做角的顶点。一般的角会假设在欧几里得平面上,但欧几里得几何中也可以定义角。角在几何学和三角学中有着广泛的应用。
几何之父欧几里得曾定义角为在平面中两条不平行的直线的相对斜度。普罗克鲁斯认为角可能是一种特质、一种可量化的量、或是一种关系。欧德谟认为角是相对直线的偏差,安提阿的卡布斯认为角是二条相交直线之间的空间 欧几里得认为角是一种关系,不过他对直角、锐角和钝角的定义都是量化的。
以上内容供参考。
角的大小与什么有关
角的大小与角的两条边张开的程度有关,与边的长短无关。角的大小决定于角的两条边张开的程度,张开的越大,角就越大,相反,张开的越小,角则越小。在动态定义中,取决于旋转的方向与角度。
一个角是由两条端点重合的射线所组成的平面图形,我们一般会将这两条射线称为是角的两条边。而两条射线所重合的端点,则会被我们叫做是角的定点。
我们一般会称两个角的角度之和等于九十度的两个角互为对方的余角,如果两角之和等于一百八十度,则会称这两个角互为补角。
所谓的对顶角指的是,有一个角的两条边的反向延长线所形成的角,就会被称作是这个角的对角。
角的大小与角的两边什么有关
角的大小与角的两条边张开的程度有关,而角的大小与边的长短没有关系。
角的大小与边的长短没有关系。张开的越大,角就越大,相反,张开的越小,角则越小。在动态定义中,取决于旋转的方向与角度。角可以分为锐角、直角、钝角、平角、周角、负角、正角、优角、劣角、0角这10种。部分角的种类如下:
1、锐角(acute angle):大于0°,小于90°的角叫做锐角。
2、直角(right angle):等于90°的角叫做直角。
3、钝角(obtuse angle):大于90°而小于180°的角叫做钝角。
4、平角(straight angle):等于180°的角叫做平角。
4、平角(straight angle):等于180°的角叫做平角。
5、优角(major angle):大于180°小于360°叫优角。
角在几何学中,是由两条有公共端点的射线组成的几何对象。这两条射线叫做角的边,它们的公共端点叫做角的顶点。一般的角会假设在欧几里得平面上,但在欧几里得几何中也可以定义角。角在几何学和三角学中有着广泛的应用。
几何之父欧几里得曾定义角为在平面中两条不平行的直线的相对斜度。普罗克鲁斯认为角可能是一种特质、一种可量化的量、或是一种关系。欧德谟认为角是相对一直线的偏差,安提阿的卡布斯认为角是二条相交直线之间的空间。欧几里得认为角是一种关系,不过他对直角、锐角和钝角的定义都是量化的。
余角和补角:两角之和为90°则两角互为余角,两角之和为180°则两角互为补角。等角的余角相等,等角的补角相等。
对顶角:两条直线相交后所得的只有一个公共顶点且两个角的两边互为反向延长线,这样的两个角叫做互为对顶角。两条直线相交,构成两对对顶角。互为对顶角的两个角相等。
邻补角:两个角有一条公共边,它们的另一条边互为反向延长线,具有这种关系的两个角,互为邻补角。
内错角:两条直线被第三条直线所截,如果两个角都在两条直线的内侧,并且在第三条直线的两侧,那么这样的一对角叫做内错角(alternate interior angle )。如:∠1和∠6,∠2和∠5。
以上就是关于角的大小与所画角的什么有关的全部内容,以及角的大小与所画角的什么有关的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。