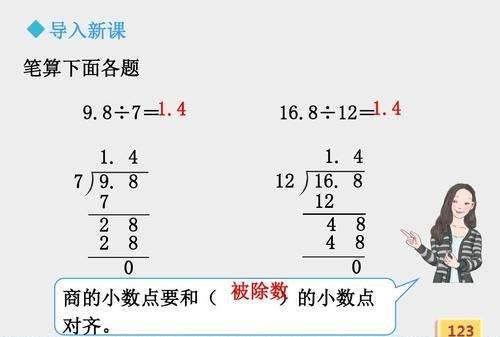
辅助角公式中的φ是怎么来的
辅助角公式中的φ是构造一个直角三角形φ就是其中的一个锐角,再利用三角函数的展开公式得到的。cosφ=a/√(a^2+b^2),φ的终边所在象限与点(a,b)所在象限相同。
三角函数辅助角公式推导:
asinx+bcosx=√(a?+b?)[asinx/√(a?+b?)+bcosx/√(a?+b?)]
令a/√(a?+b?)=cosφ,b/√(a?+b?)=sinφ
asinx+bcosx=√(a?+b?)(sinxcosφ+cosxsinφ)=√(a?+b?)sin(x+φ)
其中,tanφ=sinφ/cosφ=b/a。
辅助角公式的 φ 怎么取值
asinA+bcosA=根号下(a方+b方)sin(A+B);
asinA-bcosA=根号下(a方+b方)sin(A-B);
其中tanB=b/a;其中a,b都是正数;所求的最小角B为锐角;
辅助角公式的 φ 怎么取值
辅助角公式φ是cosφ=b/√(a^2+b^2),辅助角公式是李善兰先生提出的一种高等三角函数公式,虽然该公式已经被写入中学课本,但其几何意义却鲜为人知。
将已知数或已知式考虑成某个自变量的三角函数值,这个自变量叫做辅助角,从辅助角的所有可能值的集合中取出一个完全确定的值,辅助角的三角函数的给定值,可以完全确定,并且在以后的变换式中就看成是已知的。
辅助角公式中的φ是怎么求
辅助角公式中的φ是怎么来的如下:
常用的辅助角公式只有一个是:asinx+bcosx=√(a2+b2)sin[x+\arctan(b/a)],辅助角公式是李善兰先生提出的一种高等三角函数公式。
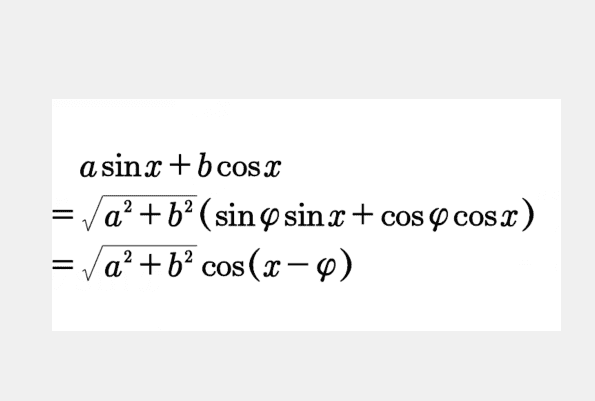
辅助角公式的主要作用是将多个三角函数的和化成单个函数,以此来求解有关最值问题。

很多人在利用辅助角公式时,经常忘记反正切到底是b/a还是a/b,导致做题出错。其实有一个很方便的记忆技巧,就是不管用正弦还是余弦来表示asinx+bcosx,分母的位置永远是你用来表示函数名称的系数。
提出者:
李善兰,原名李心兰,字竟芳,号秋纫,别号壬叔。出生于1811年 1月22日,逝世于1882年12月9日,浙江海宁人,是中国近代著名的数学、天文学、力学和植物学家,创立了二次平方根的幂级数展开式,研究各种三角函数,反三角函数和对数函数的幂级数展开式(现称“自然数幂求和公式”),这是李善兰也是19世纪中国数学界最重大的成就。
相关如下
辅助角公式推理过程:
asinx+bcosx
=√(a^2+b^2){sinx*(a/√(a^2+b^2)+cosx*(b/√(a^2+b^2)}
=√(a^2+b^2)sin(x+φ)
所以:cosφ=a/√(a^2+b^2) 或者 sinφ=b/√(a^2+b^2) 或者 tanφ=b/a(φ=arctanb/a )
其实就是运用了sin的二倍角公式(逆过程,即倒推),要验证一下的话,就用sin^2+cos^2=1。
辅助角公式的 φ怎么确定正负
辅助角公式φ怎么计算:
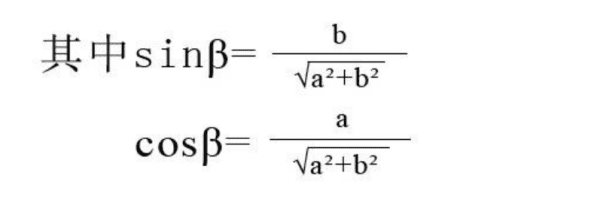
求辅助角公式φ公式:cosφ=a/√(a^2+b^2)。辅助角公式是李善兰先生提出的一种高等三角函数公式,使用代数式表达为asinx+bcosx=√(a²+b²)sin(a>0)。虽然该公式已经被写入中学课本,但其几何意义却鲜为人知。
三角函数是基本初等函数之一,是以角度(数学上最常用弧度制,下同)为自变量,角度对应任意角终边与单位圆交点坐标或其比值为因变量的函数。也可以等价地用与单位圆有关的各种线段的长度来定义。三角函数在研究三角形和圆等几何形状的性质时有重要作用,也是研究周期性现象的基础数学工具。

以上就是关于辅助角公式的φ怎么取值,辅助角公式中的φ是怎么来的的全部内容,以及辅助角公式中的φ是怎么来的的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。