共线向量怎么表示
共线向量(Parallelvector)也就是平行向量,方向相同或相反的非零向量叫平行向量,表示为a∥b,任意一组平行向量都可移到同一直线上,所以称为共线向量。
共线向量基本定理为如果a≠0,那么向量b与a共线的充要条件是:存在唯一实数λ,使得b=λa。
向量共线的公式
向量共线的公式是:向量m=(a,b),向量n=(c,d)。
两者共线时ad=bc。若向量a与向量b(b为非零向量)共线,则a=λb(λ为实数)。向量a与向量b共线的充要条件是,a与b线性相关,即存在不全为0的两个实数λ和μ,使λa+μb=0。更一般的,平面内若a=(p1,p2),b=(q1,q2),a∥b的充要条件是p1·q2=p2·q1。
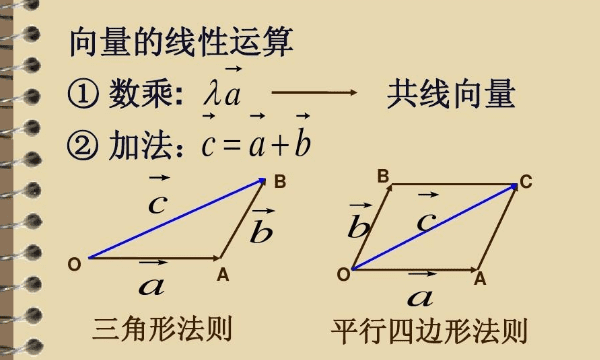
数学中的向量共线
1、在数学中,向量(也称为欧几里得向量、几何向量、矢量),指具有大小(magnitude)和方向的量。它可以形象化地表示为带箭头的线段。箭头所指:代表向量的方向;线段长度:代表向量的大小。与向量对应的只有大小,没有方向的量叫做数量(物理学中称标量)。
2、在空间直角坐标系中,也能把向量以数对形式表示,例如Oxy平面中(2,3)是一向量。 在物理学和工程学中,几何向量更常被称为矢量。许多物理量都是矢量,比如一个物体的位移,球撞向墙而对其施加的力等等。与之相对的是标量,即只有大小而没有方向的量。一些与向量有关的定义亦与物理概念有密切的联系,例如向量势对应于物理中的势能。
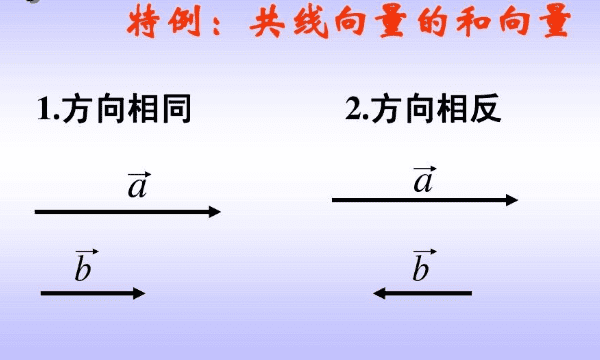
3、几何向量的概念在线性代数中经由抽象化,得到更一般的向量概念。此处向量定义为向量空间的元素,要注意这些抽象意义上的向量不一定以数对表示,大小和方向的概念亦不一定适用。因此,平日阅读时需按照语境来区分文中所说的"向量"是哪一种概念。
如何证明两向量共线?
共线向量基本定理为如果 a≠0,那么向量b与a共线的充要条件是:存在唯一实数λ,使得 b=λa。
证明:
1、充分性:对于向量 a(a≠0)、b,如果有一个实数λ,使 b=λa,那么由实数与向量的积的定义 知,向量a与b共线。
2、必要性:已知向量a与b共线,a≠0,且向量b的长度是向量a的长度的m倍,即 ∣b∣=m∣a∣。那么当向量a与b同方向时,令 λ=m,有 b =λa,当向量a与b反方向时,令 λ=-m,有 b=λa。如果b=0,那么λ=0。
3、唯一性:如果 b=λa=μa,那么 (λ-μ)a=0。但因a≠0,所以 λ=μ。
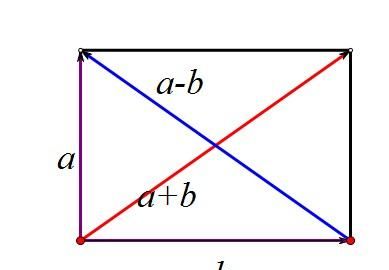
扩展资料:
向量的记法:
印刷体记作黑体(粗体)的字母(如a、b、u、v),书写时在字母顶上加一小箭头“→”。 [1] 如果给定向量的起点(A)和终点(B),可将向量记作AB(并于顶上加→)。在空间直角坐标系中,也能把向量以数对形式表示,例如xOy平面中(2,3)是一向量。
几何向量的概念在线性代数中经由抽象化,得到更一般的向量概念。此处向量定义为向量空间的元素,要注意这些抽象意义上的向量不一定以数对表示,大小和方向的概念亦不一定适用。因此,平日阅读时需按照语境来区分文中所说的"向量"是哪一种概念。
不过,依然可以找出一个向量空间的基来设置坐标系,也可以透过选取恰当的定义,在向量空间上介定范数和内积,这允许我们把抽象意义上的向量类比为具体的几何向量。
平面向量的共线表示
平面向量的共线为:向量m=(a,b),向量n=(c,d),两者共线时 ad=bc。
平面向量共线定理:共线向量也就是平行向量,方向相同或相反的非零向量叫平行向量,表示为a∥b ,任意一组平行向量都可移到同一直线上,所以称为共线向量。
共线向量基本定理为如果a≠0,那么向量b与a共线的充要条件是:存在唯一实数λ,使得 b=λa。
如果a≠0,那么向量b与a共线的充要条件是:存在唯一实数λ,使得b=λa。
这项定理其实说明了平面向量可以沿任意指定的两方向分解,同时也说明了由任意两向量可以合成指定向量,即向量的合成与分解 。
平面向量的解释:
当两个方向相互垂直时,其实就是把他们在平面直角坐标系中分解,此时(x,y)就称为此向量的坐标。(此向量的起点为原点)所以此定理为向量的坐标表示提供了理论依据。
平面向量基本定理是平面向量坐标表示的基础,它说明同一平面内的任一向量都可以表示为其他两个不共线向量的线性组合。在解具体问题时适当地选取基底,使其它向量能够用基底来表示,选择两个不共线的向量 ,平面内的任何一个向量都可以唯一表示,这样几何问题就可以转化为代数问题。
以上就是关于向量共线的公式,共线向量怎么表示的全部内容,以及共线向量怎么表示的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。