向量积怎么求
向量积,数学中又称外积、叉积,物理中称矢积、叉乘,是一种在向量空间中向量的二元运算。与点积不同,它的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量和垂直。其应用也十分广泛,通常应用于物理学光学和计算机图形学中。
数量积AB=ac+bd。向量积要利用行列式。若向量a=(a1,b1,c1),向量b=(a2,b2,c2)。则向量a·向量b=a1a2+b1b2+c1c2。向量a×向量b=|ijk||a1b1c1||a2b2c2|=(b1c2-b2c1,c1a2-a1c2,a1b2-a2b1)。i、j、k分别为空间中相互垂直的三条坐标轴的单位向量。
三角形的面积公式是什么向量
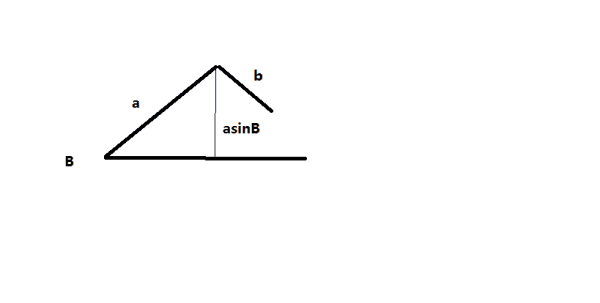
公式:|axb|/2。
两个向量a,b为边的三角形,向量的叉乘的绝对值=|a||b|sin是三角形面积两倍,|axb|/2就是三角形面积。
在数学中,向量指具有大小和方向的量。可以形象化地表示为带箭头的线段。箭头所指:代表向量的方向;线段长度:代表向量的大小。与向量对应的量叫做数量(物理学中称标量),数量(或标量)只有大小,没有方向。
应用:
1、有两个成α(0<α<180)的两个力N1、N2,把两个力首尾相连(三角形的两个边),其合力Q的方向和大小为从N1的起点到N2的终点(三角形的第三条)。
2、有N1、N2……N个力,将其顺序首尾相连,其合力Q的方向和大小为从N1的起点到N的终点。若起合力为零,则N1、N2……N首尾相连将组成一个封闭的多边形。
3、一个力N可以分解为成任意角度的两个力F1、F2,F1、F2、N组成封闭的三角形。特别的如果F1、F2分别平行于X、Y轴,则力N分解为两个平行于坐标轴的两个力FX、FY,此时,FX、FY、N组成直角三角形,N为斜边。
向量叉乘三角形面积公式
向量叉乘求三角形面积为:1/2|a*b|。设三角形两边a,b,夹角为θ,由于|a*b|=|a||b|sin(θ),|b|sin(θ)相当于三角形的高,所以三角形面积=1/2|a*b|,即两向量叉积的模的一半。
向量叉乘即向量积,数学中又称外积、叉积,物理中称矢积、叉乘,是一种在向量空间中向量的二元运算。与点积不同,它的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量和垂直。其应用也十分广泛,通常应用于物理学光学和计算机图形学中。
实数与向量的积的定义
三角形面积=1/2*|ab|*|ac|*sin∠bac=(1/2)*1*2*sin∠bac
(向量ab+向量ac)*向量ab=ab²+|ab|*|ac|*cos
∠bac=2
所以
cos
∠bac=1/2
sin
∠bac=根号三/2
所以可以求得
面积=根号三/2
高等数学向量代数与空间解析几何知识点
(1)底:a=1
高:√3*sin(π/6)
面积:S=ab=√3/2
(2)顺便回答下,没有关系(一个是标量,另一个是向量),向量积 也被称为矢量积、叉积(即交叉乘积)、外积,是一种在向量空间中向量的二元运算。与点积不同,它的运算结果是一个伪向量而不是一个标量。并且两个向量的叉积与这两个向量垂直。
PS:向量的内积、数量积最多是用来判断向量的垂直
叉积的长度 |a×b| 可以解释成以a和b为邻边的平行四边形的面积。
混合积 [a b c] = (a×b)·c可以得到以a,b,c为棱的平行六面体的体积。
以上就是关于向量积怎么,三角形的面积公式是什么向量的全部内容,以及向量积怎么求的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。