周长求半径公式是什么
周长求半径公式是R=L÷π÷2,在古典几何中,圆或圆的半径是从其中心到其周边的任何线段,并且在更现代的使用中,它也是其中任何一个的长度。
这个名字来自拉丁半径,意思是射线,也是一个战车的轮辐。
半径的复数可以是半径(拉丁文复数)或常规英文复数半径。
半径的典型缩写和数学变量名称为r。
通过延伸,直径d定义为半径的两倍:d=2r。
知道周长求半径的公式
知道周长求半径公式:r=C÷2÷π。在古典几何中,圆或圆的半径是从其中心到其周边的任何线段,并且在更现代的使用中,它也是其中任何一个的长度。这个名字来自拉丁半径,意思是射线,也是一个战车的轮辐。
圆是一种几何图形。根据定义,通常用圆规来画圆。同圆内圆的直径、半径的长度永远相同,圆有无数条半径和无数条直径。圆是轴对称、中心对称图形。对称轴是直径所在的直线。同时,圆又是“正无限多边形”,而“无限”只是一个概念。当多边形的边数越多时,其形状、周长、面积就都越接近于圆。所以,世界上没有真正的圆,圆实际上只是一种概念性的图形。
知道周长求半径的公式
知道周长求圆的半径用公式d=C/π。
在一个平面内,一动点以一定点为中心,以一定长度为距离旋转一周所形成的封闭曲线就叫做圆。圆有无数条对称轴。在同一平面内,到定点的距离等于定长的点的集合叫做圆。圆可以表示为集合{M||MO|=r},其中O是圆心,r 是半径。圆的标准方程是(x - a) ² + (y - b) ² = r ²,其中点(a,b)是圆心,r是半径。
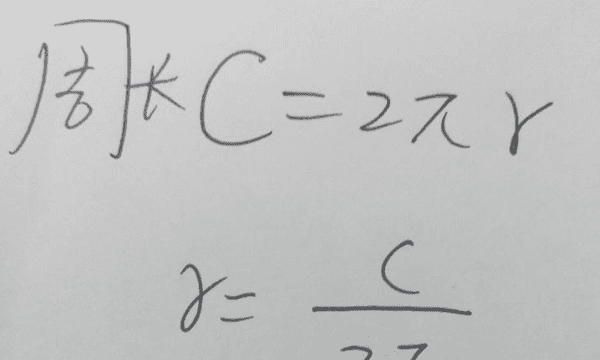
半径公式:
1、圆的半径公式:r=1/2√(D2+E2-4F)。
2、圆的一般方程是:x2+y2+Dx+Ey+F=0(D2+E2-4F>0),其中圆心坐标是(-D/2,-E/2)。
3、扇形弧长L=圆心角(弧度制)×R= nπR/180(θ为圆心角)(R为扇形半径)。
4、扇形面积S=nπ R2/360=LR/2(L为扇形的弧长)。
5、圆锥底面半径 r=nR/360(r为底面半径)(n为圆心角)。
几何圆的解释
在一个平面内,围绕一个点并以一定长度为距离旋转一周所形成的封闭曲线叫作圆(Circle),全称圆形。在平面内,圆是到定点的距离等于定长的点的集合叫作圆(Circle)。圆有无数条对称轴,对称轴经过圆心。圆具有旋转不变性。圆形是一种圆锥曲线,由平行于圆锥底面的平面截圆锥得到。
圆形规定为360°,是古巴比伦人在观察地平线太阳升起的时候,大约每4分钟移动一个位置,一天24小时移动了360个位置,所以规定一个圆内角为360°。这个°,代表太阳。圆是一种几何图形。根据定义,通常用圆规来画圆。 同圆内圆的直径、半径的长度永远相同,圆有无数条半径和无数条直径。圆是轴对称、中心对称图形。
已知周长半径公式是什么
已知周长求半径公式:r=C/2π。

首先,我们知道圆的周长(C)与半径(r)之间的关系式为:
C=2πr
其中,C 是圆的周长,π 是圆周率(约等于3.14159),r 是圆的半径。
如果我们知道圆的周长(C=2πr),那么我们可以将它转化为:
r=C/2π。
这个公式可以帮助我们根据已知的周长求出圆的半径。这里的π是一个无限不循环小数,通常在计算中我们使用近似值3.14或22/7。
现在,让我们通过一个具体的例子来说明如何使用这个公式:
例子: 假设一个圆的周长是20厘米,我们要求这个圆的半径。

根据上面的公式,我们可以将已知的周长(C=20厘米)代入公式中,进行计算,我们得到:
r≈3.18厘米。
所以,已知圆的周长为20厘米时,这个圆的半径约为3.18厘米。
这个公式不仅适用于计算圆的半径,也可以用来计算其他与圆相关的参数。
总结而言,通过已知圆的周长,我们可以利用上述公式求出圆的半径,这是解决与圆周长相关问题的一种基本方法。这个公式的应用不仅仅局限于数学课堂,也可以在日常生活和实际问题中用来解决各种计算需求。
以上就是关于周长半径公式是什么,知道周长求半径的公式的全部内容,以及周长求半径公式是什么的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。