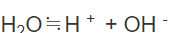函数的表示法有哪几种
函数的表示法有列表法、解析式法、图象法。
1、列表法:一目了然,使用起来方便,但列出的对应值是有限的,不易看出自变量与函数之间的对应规律。列表法也有它的局限性:在于求解范围小,适用题型狭窄,大多跟寻找规律或显示规律有关。
2、解析式法:简单明了,能够准确地反映整个变化过程中自变量与函数之间的相依关系,但有些实际问提中的函数关系,不能用解析式表示。
3、图象法:形象直观,但只能近似地表达两个变量之间的函数关系。把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标,在直角坐标系内描出它的对应点,所有这些点组成的图形叫做该函数的图象。这种表示函数关系的方法叫做图象法。
函数有哪三种表示方法?
表示函数有三种方法:解析法,列表法,图象法.结合其意义,优点与不足,分别说明如下. (1)利用解析式(如学过的代数式)表示函数的方法叫做解析法.用解析式表示函数的优点是简明扼要,规范准确.已学利用函数的解析式,求自变量x=a时对应的函数值,还可利用函数的解析式,列表,描点,画函数的图象,进而研究函数的性质,又可利用函数解析式的结构特点,分析和发现自变量与函数间的依存关系,猜想或推导函数的性质(如对称性,增减性等),探求函数的应用等.不足之处是有些变量与函数关系很难或不能用解析式表示,求x与y的对应值需要逐个计算,有时比较繁杂. (2)通过列表给出y与x的对应数值,表示y是x的函数的方法叫做列表法.列表法的优点是能鲜明地显现出自变量与函数值之间的数量关系,于是一些数学用表应运而生. (3)利用图象表示y是x的函数的方法叫做图象法.用图象表示函数的优点是形象直观,清晰呈现函数的增减变化,点的对称,最大(或小)值等性质.图象法的不足之处是所画出的图象是近似的,局部的,观察或由图象确定的函数值往往不够准确. 由于函数关系的三种表示方法各具特色,优点突出,但大都存在着缺点,不尽人意,所以在应用中本着物尽其用,扬长避短,优势互补的精神,通常表示函数关系是把这三种方法结合起来运用,先确定函数的解析式,即用解析法表示函数;再根据函数解析式,计算自变量与函数的各组对应值,列表;最后是画出函数的图象.
三种表示函数的方法各有什么优点
三种表示函数的方法是符号法、图像法和表格法。
一、符号法(Symbolic Representation)
以数学符号的形式来表示函数,常用的符号包括字母、数字、运算符号等。通过符号表达,可以清晰地描述函数的定义域、值域、性质等。
1.函数的定义:通常用$f(x)$或$y=f(x)$表示函数,其中$x$为自变量,$y$为函数值。例如,$f(x)=2x+1$表示一个线性函数。
2.函数的运算:使用符号法可以进行各种函数运算,如加法、减法、乘法、除法、复合运算等。例如,设有函数$f(x)=2x+1$和$g(x)=x^2$,则它们的加法运算为$(f+g)(x)=(2x+1)+(x^2)$。
3.函数的性质:符号法还可以用于描述函数的性质,如奇偶性、单调性、周期性等。例如,对于函数$f(x)=\sin(x)$,可以通过符号法表达出它的周期性为$2\pi$。
二、图像法(Graphical Representation)
通过绘制函数的图像来表示函数,通过观察函数的图像可以更直观地了解函数的特征。
1.坐标系:图像法需要利用平面直角坐标系来绘制函数图像,其中横轴表示自变量$x$,纵轴表示函数值$y$。
2.轨迹:函数的图像是由一系列点组成的曲线或折线,这些点坐标的集合就是函数的图像。例如,对于函数$f(x)=x^2$,它的图像是一个抛物线。
3.特征:通过观察函数图像可以了解函数的性质,如增减性、极值、拐点等。例如,对于函数$f(x)=x^3$,通过观察其图像可以得知它在原点处有一个拐点。
三、表格法(Tabular Representation)
将函数的自变量和函数值制成表格形式来表示函数,通过表格可以方便地整理和查找函数值。
1.自变量与函数值:将自变量和函数值按照对应关系排列成表格,自变量通常从小到大排列。
2.函数性质:表格法也可以用于记录和计算函数的性质。例如,可以通过表格法计算函数$f(x)=\frac{1}{x}$在不同自变量取值下的函数值。
3.插值和外推:利用表格法可以进行插值和外推,即通过已知的函数值来估计未知的函数值。例如,通过已知表格中的一些值,可以估计出函数$f(x)=\sin(x)$在其他自变量取值下的函数值。
以上就是关于函数的表示法有哪几种,函数有哪三种表示方法?的全部内容,以及函数的表示法有哪几种的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。