双曲线c是什么
双曲线c表示焦点位置。一般的,双曲线(希腊语“?περβολ?”,字面意思是“超过”或“超出”)是定义为平面交截直角圆锥面的两半的一类圆锥曲线。
双曲线可以定义为与两个固定的点(叫做焦点)的距离差是常数的点的轨迹。这个固定的距离差是a的两倍,这里的a是从双曲线的中心到双曲线最近的分支的顶点的距离。a还叫做双曲线的实半轴。焦点位于贯穿轴上,它们的中间点叫做中心,中心一般位于原点处。
双曲线中的abc分别表示什么
a为实半轴长,b为虚半轴长,c为半焦距。
双曲线上的一点到定点的距离和到定直线(相应准线)的距离的比等于双曲线的离心率。双曲线焦半径公式:圆锥曲线上任意一点到焦点距离。
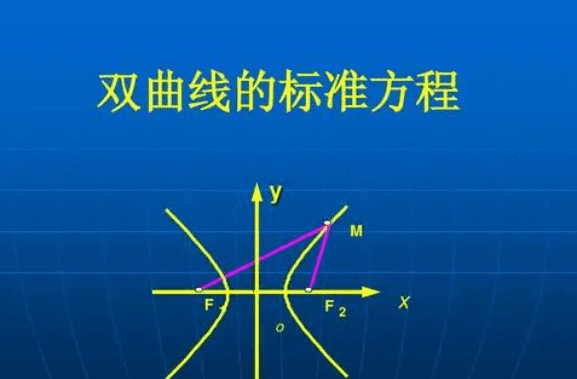
实际应用
双曲线在实际中的应用有通风塔,冷却塔,埃菲尔铁塔,广州塔等。
顶点
双曲线和它的焦点连线所在直线有两个交点,它们叫做双曲线的顶点。
实轴
两顶点之间的线段称为双曲线的实轴,实轴长的一半称为半实轴。
虚轴
在标准方程中令x=0,得y²=-b²,该方程无实根,为便于作图,在y轴上画出B1(0,b)和B2(0,-b),以B1B2为虚轴。
双曲线中的abc是什么意思
a是实轴顶点到双曲线中心的距离,b是虚轴顶点到双曲线中心的距离,c是焦点到双曲线中心的距离,a,b,c满足a^2+b^2=c^2
双曲线abc分别代表什么
双曲线的abc分别指:a表示双曲线右支的顶点位置,c表示焦点位置,b表示虚轴的一半。a^2+b^2=c^2,渐近线与x轴还有过双曲线与x轴交点并垂直于x轴的直线组成的一个直角三角形的条边分别对应a、b、c。
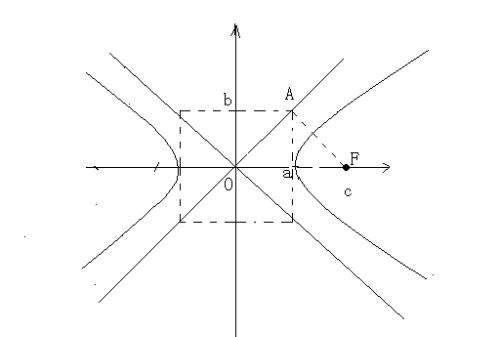
双曲线的其他概念:
1、A(-a,0),A'(a,0)。同时AA'叫做双曲线的实轴且│AA'│=2a。
2、B(0,-b),B'(0,b)。同时BB'叫做双曲线的虚轴且│BB'│=2b。
3、F1(-c,0)或(0,-c),F2(c,0)或(0,c)。F1为双曲线的左焦点,F2为双曲线的右焦点且│F1F2│=2c。
4、离心率,第一定义:e=c/a且e∈(1,+∞)。
双曲线中的abc表示什么图解
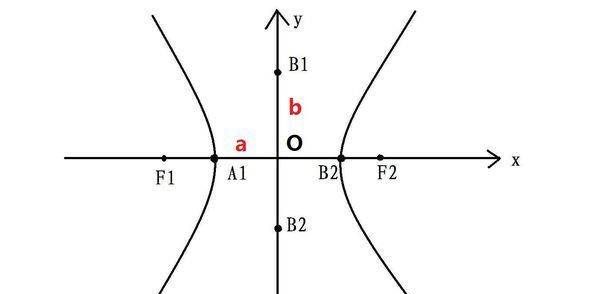
双曲线x²/a²-y²/b²=1,其中a代表双曲线顶点到原点的距离(实半轴),b代表双曲线的虚半轴,c代表焦点到原点的距离(半焦距),a,b,c满足关系式a²+b²=c²。
其中:OA1=a,OB1=b,OF1=c。O为原点。
我们把平面内与两个定点F1,F2的距离的差的绝对值等于一个常数(常数为2a,小于|F1F2|)的轨迹称为双曲线;平面内到两定点的距离差的绝对值为定长的点的轨迹叫做双曲线),即:│|PF1|-|PF2│|=2a。
相关信息:
双曲线的其他概念:
(1)A(-a,0),A'(a,0)。同时AA'叫做双曲线的实轴且│AA'│=2a。
(2)B(0,-b),B'(0,b)。同时BB'叫做双曲线的虚轴且│BB'│=2b。
(3)F1(-c,0)或(0,-c),F2(c,0)或(0,c)。F1为双曲线的左焦点,F2为双曲线的右焦点且│F1F2│=2c。
(4)离心率,第一定义:e=c/a且e∈(1,+∞)。
以上就是关于双曲线c是什么,双曲线中的abc分别表示什么的全部内容,以及双曲线c是什么的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。


