如何确定一个圆
确定一个圆需要有圆心和半径。
圆是一种几何图形。
根据定义,通常用圆规来画圆。
同圆内圆的直径、半径的长度永远相同,圆有无数条半径和无数条直径。
圆是轴对称、中心对称图形。
对称轴是直径所在的直线。
同时,圆又是“正无限多边形”,而“无限”只是一个概念。
当多边形的边数越多时,其形状、周长、面积就都越接近于圆。
所以,世界上没有真正的圆,圆实际上只是概念性的图形。
怎样用圆规确定圆的圆心
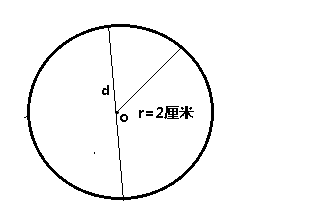
可以利用圆规画图,在纸上确定一个圆心并用圆规在直齿上量出两厘米,将圆规的针置于之前的圆心上,在纸上将圆画出来。如下图所示。
扩展资料
圆的基本构成有圆心和半径, 它们对圆起到确定位置和尺寸的作用。
当一条线段绕着它的一个端点在平面内旋转一周时,它的另一个端点的轨迹叫做圆。
在同一平面内,到定点的距离等于定长的点的集合叫做圆。
圆是一种几何图形。根据定义,通常用圆规来画圆。 同圆内圆的半径长度永远相同,圆有无数条半径和无数条直径。圆是轴对称、中心对称图形。对称轴是直径所在的直线。
同时,圆又是“正无限多边形”,而“无限”只是一个概念。当多边形的边数越多时,其形状、周长、面积就都越接近于圆。所以,世界上没有真正的圆,圆实际上只是概念性的图形。
各类圆的各种计算公式(其中半径为r、圆周率为π、直径为d、R为大半径、h为高)
1、圆的面积:πr^2
2、圆的周长:2πr
3、半圆的周长:πr+2r
4、圆环的面积:(R^-r^)π
5、圆柱的体积:πr^2h
6、圆柱的表面积:πr^2*2+πdh
7、圆环的体积:(R^2-r^2)πh
怎样确定一个圆的圆心?有几种方法?
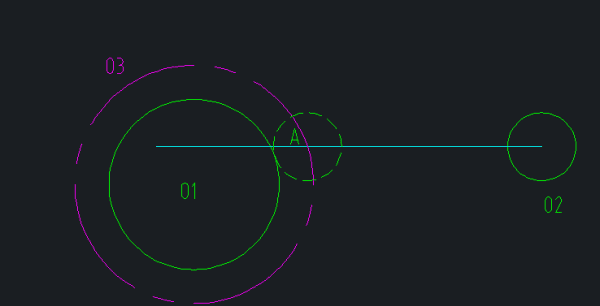
固定圆O1,移动圆O2。
1、以O1圆为圆心,以两圆半径之和为半径画圆O3(图中洋红点画线),交O2平移线于点A;
2、以A为圆心,O2半径值为半径画圆,即为所求圆。
解读:确定圆心位置是关键,首先圆心肯定是在要求的平移线上;
当两圆相切时,O3圆可以看作是O2围绕O1作相切运动的轨迹圆。那么O2的圆心肯定是在O3这条轨迹线上的。
所以满足这两个条件的交集,即平移线与O3相交的点,即为所求圆的圆心位置,可解。
三点如何确定一个圆心
连结3点,形成三角形,再作任意两边的垂直平分线,交于一点,该点即为圆心,且到三点距离相等。
第一步:首先假设圆心为(x0, y0),半径为r。
第二步:假设知道的三个点为(x1,y1),(x2,y2),(x3,y3)。
第三步:确定这个方程是不是有解。
第四步:设两个常量a1,a2。
第五步:解出该圆的圆心坐标,既两条中垂线的交点坐标。
在同一平面内,到定点的距离等于定长的点的集合叫做圆。圆可以表示为集合{M||MO|=r},圆的标准方程是(x - a) ² + (y - b) ² = r ²。其中,o是圆心,r 是半径。
圆形是一种圆锥曲线,由平行于圆锥底面的平面截圆锥得到。
扩展资料:
圆是一个正n边形(n为无限大的正整数),边长无限接近0但永远无法等于0。假设定点为A,B,动点为P,满足|PA|/|PB| = k(k≠1),过P点作角APB的内、外角平分线,交AB与AB的延长线于C,D两点由角平分线性质,角CPD=90°。
由角平分线定理:PA/PB = AC/BC = AD/BD =k,注意到唯一k确定了C和D的位置,C在线段AB内,D在AB延长线上,对于所有的P,P在以CD为直径的圆上。
直线和圆位置关系:
①直线和圆无公共点,称相离。 AB与圆O相离,d>r。
②直线和圆有两个公共点,称相交,这条直线叫做圆的割线。AB与⊙O相交,d ③直线和圆有且只有一公共点,称相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点。圆心与切点的连线垂直于切线。AB与⊙O相切,d=r。 以上就是关于如何确定一个圆,怎样用圆规确定圆的圆心的全部内容,以及如何确定一个圆的相关内容,希望能够帮到您。 版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。