正多边形边数公式是什么
正多边形边数的公式:
1、已知多边形的内角和,求边数的公式:n边形的边=(内角和÷180°)+2。
2、已知多边形的内外角的差,求边数的公式:边数=(内外角差+360°)÷180°+2。
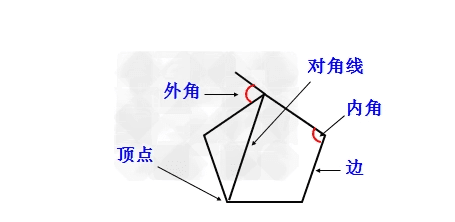
由三条或三条以上的线段首尾顺次连接所组源成的平面图形叫做多边形。组成多边形的线段至少有3条,三角形是最简单的多边形。组成多边形的每一条线段叫做多边形的边;相邻的两条线段的公共端点叫做多边形的顶点;多边形相邻两边所组成的角叫做多边形的内角;连接多边形的两个不相邻顶点的线段叫做多边形的对角线。
正多边形的边数怎么算
多边形边数公式:n边形的边=(内角和÷180°)+2。
此定理适用所有的平面多边形,包括凸多边形和平面凹多边形。
多边形角度公式:
1、n边形外角和等于n·180°-(n-2)·180°=360°。
2、多边形的每个内角与它相邻的外角是邻补角,所以n边形内角和加外角和等于n·180°。
3、内角:正n边形的内角和度数为:(n-2)×180°;正n边形的一个内角是(n-2)×180°÷n。
内角,数学术语,多边形相邻的两边组成的角叫做多边形的内角。
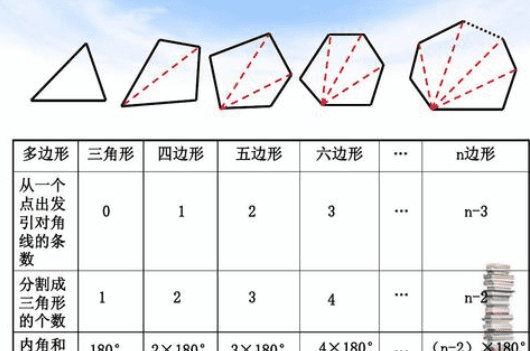
在数学中,三角形内角和为180°,四边形(多边形)内角和为360°。以此类推,加一条边,内角和就加180°。
内角和公式为:(n - 2)×180° 正多边形各内角度数为: (n - 2)×180°÷n
例如三角形内角和就是一个△内部的三个角的和,一个内角就是其中任意一个角。
正多边形的边数怎样确定图片
多边形边数公式:n边形的边=(内角和÷180°)+2。
此定理适用所有的平面多边形,包括凸多边形和平面凹多边形。
多边形角度公式:
1、n边形外角和等于n·180°-(n-2)·180°=360°。
2、多边形的每个内角与它相邻的外角是邻补角,所以n边形内角和加外角和等于n·180°。
3、内角:正n边形的内角和度数为:(n-2)×180°;正n边形的一个内角是(n-2)×180°÷n。
扩展资料:
各边相等,各角也相等的多边形叫做正多边形。
正多边形的外接圆的圆心叫做正多边形的中心。
正多边形的外接圆的半径叫做半径。
中心到圆内接正多边形各边的距离叫做边心距。
正多边形各边所对的外接圆的圆心角都相等,这个圆心角叫做正多边形的中心角。
正多边形边数公式
正多边形的边数公式为:n = 4 × tan(π/n),其中,n 表示正多边形的边数,π表示圆周率。
正多边形边数公式是由希腊数学家阿基米德(Archimedes)在他著名的《圆的测量》(Measurement of the Circle)一书中首次给出的。在这本书中,阿基米德利用弧长逐渐逼近多边形的方法,推导出了圆周率的逼近值。利用这种方法,阿基米德还推导出了正多边形的周长公式和面积公式。

正多边形边数公式是由周长和半径之间的关系推导而来的。由于正多边形的边和半径都相等,因此正多边形的周长直接与其边长成正比。而正多边形内角和总是等于 (n - 2)×180 度,每个内角又都是 360 度除以边数 n,因此可以得到每个内角为 (n - 2) × 180 / n 度。
由于正多边形的内角为圆心角,因此可以通过三角函数来计算正多边形的边长。因此,利用周长和内角的关系以及三角函数,阿基米德就推导出了正多边形边数公式。正多边形边数公式可以用于计算正多边形的边数,也可以用于其他相关问题的计算。

常见正多边形的边数
1、三角形(Equilateral triangle):3个边。
2、四边形(Square):4个边。
3、五边形(Pentagon):5个边。
4、六边形(Hexagon):6个边。
5、七边形(Heptagon):7个边。
6、八边形(Octagon):8个边。
7、九边形(Nonagon):9个边。
8、十边形(Decagon):10个边。
9、十二边形(Dodecagon):12个边。
10、二十边形(Icosagon):20个边。
以上就是关于正多边形的边数怎么算,正多边形边数公式是什么的全部内容,以及正多边形边数公式是什么的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。