根号2的被开方数是多少
根号2的被开方数是四次根号2,根号是一个数学符号。
根号是用来表示对一个数或一个代数式进行开方运算的符号。
若a^n=b,那么a是b开n次方的n次方根或a是b的1/n次方。
开n次方手写体和印刷体用√ ̄表示,被开方的数或代数式写在符号左方v形部分的右边和符号上方一横部分的下方共同包围的区域中,而且不能出界。
根号2怎么算的过程教学视频
根号2的计算过程教学如下:
写出根号2的表达式。根号2的规范写法是“√2”,其中“2”写在右下角。将根号2的被开方数2写在一个空白处。找出完全平方数。完全平方数是指能够写成两个整数的平方和的数。在这个例子中,我们需要找到一个能够被2整除的数,使得它的平方和等于根号2的被开方数2。通过观察,我们发现1的平方和1^2 = 1,而1.4142135623730950488016887242096980785696718753769480731766797379907324784621的平方和1.96更接近2。
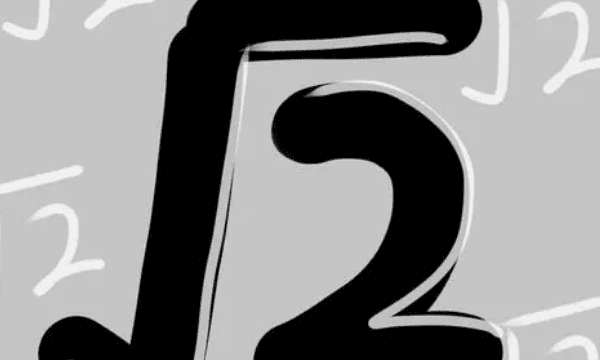
将完全平方数乘以它自己,得到平方的结果。在这个例子中,我们计算1^2 = 1,以及1.4142135623730950488016887242096980785696718753769480731766797379907324784621^2。比较完全平方数和平方的结果,看它们是否接近根号2的被开方数。在这个例子中。1.4142135623730950488016887242096980785696718753769480731766797379907324784621的平方更接近根号2的被开方数。通过以上步骤,我们可以得出根号2的值,约为1.414。
学习数学的好处:
1、逻辑思维
数学是一门需要推理和逻辑思维的学科。通过学习数学,我们可以培养和发展自己的逻辑思维能力和解决问题的能力。这种逻辑思维能力不仅在数学学习中有用,而且在很多其他领域,如科学、工程、经济等都有广泛的应用。

2、解决问题的能力
数学问题的解决通常需要一种创新和灵活的思维方式。通过解决数学问题,我们可以学习到如何分析问题、如何寻找解决问题的策略,以及如何从错误中学习。这种解决问题的能力在现实生活中是非常重要的,无论是在学习、工作还是日常生活中。
3、创造力和想象力
数学是一门需要创造性和想象力的学科。通过学习数学,我们可以学习到如何从不同的角度去看待问题,如何发现和创造新的想法。这种创造力和想象力不仅在数学中有用,在艺术、文学、科学等其他领域也非常重要。
根号2的计算方法基础
一
(√2+1)(√2-1)=2-1=1 √2-1=1/(√2+1)
√2 = 1+1/(√2+1)= 1+1/(2+√2-1)= 1+1/[2+1/(√2+1)]=1+1/[2+1/(2+√2-1)]=1+1/{2+1/[2+1/(√2+1)}
后面就是循环问题了,越往下换算就越精确,计算的时候,把最后分母的√2+1换成2,而且2的个数要为偶数。这样结果比真实值小,但已经很靠近真实值了
二
假设被开方数为a,那么[√x-√(a/x)]^2=0的根就是√a
展开得x-2√a+a/x=0 x^2-2x√a+a=0 x^2+a=2x√a
变形得 √a=(x+a/x)/2
所以只需设置一个约等于(x+a/x)/2的初始值,代入上面公式,可以得到一个更加近似的值,再将它代入,就得到一个更加精确的值……依此方法,最后得到一个足够精度的(x+a/x)/2的值。
用逐次逼近的方法求根号2的近似值
(1)X1=1 (2)X2=1/2(X1+2/X1) (3)X3=1/2(X2+2/X2) (4)X4=1/2(X3+2/X3)
X1=1 X2=1/2(1+2)=3/2=1.5 X3=17/12=1.41666... X4=577/408=1.41421568627451
√2≈1.41421356237309,前六位相同,越往下换算就越精确
三
试算法,即先设定一个值,再计算其与所求值的误差,并进行调整后,进入下一轮试算,直到最后算出的误差满足小数点后几位的精度为止.
我们知道面积是2的正方形的边长是√2,设√2=1+x,有1+2x﹢x^2=2,但x是较小的数略去x^2,得1+2x≈2,解得x≈0.5,即√2≈1.5.
再设√2=1.5+y,同样道理,有1.5^2+2×1.5y≈2,解得y≈-0.0833,即√2≈1.4167
再设√2=1.4167+z,同样道理,有1.4167^2+2×1.4167y≈2,解得z≈-0.0024842,即√2=1.4167+z≈1.4167-0.0024842=1.4142158
按所述的方法代入即设1.4142158^2+2×1.4142158a≈2,解得a=-0.000002238,即√2=1.4142158-0.000002238=1.414213562.
四
笔算开平方法的计算步骤如下:
1.将被开方数的整数部分从个位起向左每隔两位划为一段,用撇号分开,分成几段,表示所求平方根是几位数;小数部分从最高位向后两位一段隔开,段数以需要的精度+1为准。
2.根据左边第一段里的数,求得平方根的最高位上的数。
3.从第一段的数减去最高位上数的平方,在它们的差的右边写上第二段数组成第一个余数。
4.把求得的最高位数乘以20去试除第一个余数,所得的最大整数作为试商
5.用商的最高位数的20倍加上这个试商再乘以试商.如果所得的积小于或等于余数,试商就是平方根的第二位数;如果所得的积大于余数,就把试商减小再试,得到的第一个小于余数的试商作为平方根的第二个数。
6.用同样的方法,继续求平方根的其他各位上的数。
如遇开不尽的情况,可根据所要求的精确度求出它的近似值.
笔算开平方运算较繁,在实际中直接应用较少,但用这个方法可求出一个数的平方根的具有任意精确度的近似值.
以上就是关于根号2的被开方数是多少,根号2怎么算的过程教学视频的全部内容,以及根号2的被开方数是多少的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。