怎么判断三角形解的个数
按正弦定理判断,如:已知三角形的两边抄a,b及b边所对的角θ,则有:a/sina=b/sinθ,sina=(asinθ)/b;若θ百≥90?则有一解度;若θ<90?b>a有一解;若b<a∠B<∠A有2个解。
正弦定理是三角学中的一个基本定理,它指出“在任意一个平面三角形中,各边和它所对角的正弦值的比相等且等于外接圆的直径”。
如何判断三角形有几解的问题
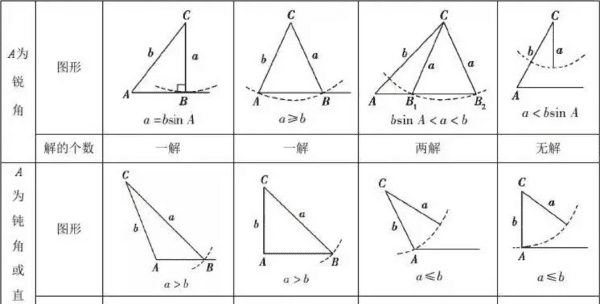
当告诉或者求出的条件满足三角形全等的几种情况之一时,三角形有唯一解,比如:边边边;边角边;角边角;角角边。以上都是唯一解但是,对于条件【边边角】当已知角为钝角或直角时为唯一解;但是已知角为锐角时则有两解。
三角形解的个数的判断方法正弦定理
画图法:以已知角的对边为半径画弧,通过与邻边的交点个数判断解的个数。
①若无交点,则无解;
②若有一个交点,则有一个解;
③若有两个交点,则有两个解;
④若交点重合,虽然有两个交点,但只能算作一个解。
公式法:运用正弦定理进行求解。
①a=bsinA,△=0,则一个解;
②a>bsinA,△>0,则两个解;
③a<bsinA,△<0,则无解。
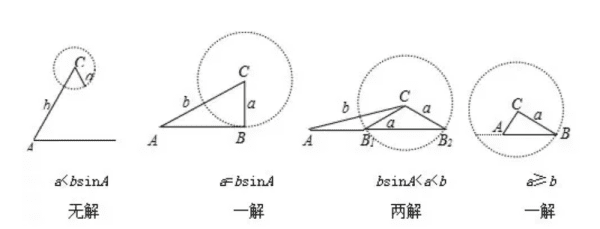
a>b 一个解 (a b是三角形的边) 利用正弦定理解三角形,假如解得sinA=c,(其中c是一个具体数字),而且没有任何额外的条件,那么就会有两个解:即A=arcsin(c)或A=π-arcsin(c)。
但是假如有别的条件或者要求,那么A的取值可能就只有一个。举个例子,如果sinA=1/2,但是sinB=√2/2,那么这时A的取值就只能是arcsin(1/2)=π/6,而不再可能取值为A=π-arcsin(1/2)=5π/6。原因是这时不管B的取值为arcsin(√2/2)=π/4或者3π/4都会使得A+B>π,与三角形内角和等于π矛盾,所以A=π/6。
当然,如果有其它条件比如已知a为最长边,那么同样有可能去掉A的一个可能的取值,比如上面的A在这种情况下就不可能取π/6(因为A应该是最大角,所以一定会大于π/3)。总之,如果除了sinA=c之外还有条件或者限制,那么A可能就只有一个解,否则就是有两个解。
如何判断三角形有几个解正弦定理
根据条件去画三角形,如果是唯一的,三角形就有唯一解。
如果能够画出不同的两个三角形,三角形就有两个解。
选项C就有两个解。
有关如何判断三角形解的个数的问题
由正弦定理:a/sin
A=b/sin
B
(2√3)
/sin
30°=b/sin
B
(2√3)
/(1/2)=b/sin
B
(2√3)
X2=b/sin
B
b=4√3sin
B
由于角A=30度,所以角B<180-30=150度
当b≤2√3时,角B≤30°有一解;
当b=4√3时,角B=90°有一解;
当2√3
当b>4√3时,无解。
以上就是关于怎么判断三角形解的个数,如何判断三角形有几解的问题的全部内容,以及怎么判断三角形解的个数的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。





