两个向量的向量积怎么求
两个向量的向量积的求法是:两个向量a和b的叉积写作a×b,叉积可以定义为a×b=absinθn。在这里θ表示a和b之间的角度(0°≤θ≤180°),位于这两个矢量所定义的平面上。而n是一个与a、b所在平面均垂直的单位矢量。
向量积,也被称为叉积(即交叉乘积)、外积,是一种在向量空间中向量的二元运算。与点积不同,它的运算结果是一个伪向量而不是一个标量。并且两个向量的叉积与这两个向量都垂直。
向量积公式怎么算
向量积公式为:A=(x1,y1,z1),B=(x2,y2,z2),A与B的数量积为x1x2+y1y2+z1z2。
向量积,数学中又称外积、叉积,物理中称矢积、叉乘,是一种在向量空间中向量的二元运算。
在数学中,向量(也称为欧几里得向量、几何向量、矢量),指具有大小和方向的量。可以形象化地表示为带箭头的线段。箭头所指:代表向量的方向;线段长度:代表向量的大小。与向量对应的量叫做数量(物理学中称标量),数量(或标量)只有大小,没有方向。
向量的乘积怎么
向量a乘以向量b=(向量a得模长)乘以(向量b的模长)乘以cosα[α为2个向量的夹角]。向量a(x1,y1)向量b(x2,y2),向量a乘以向量b=(x1*x2,y1*y2)。
向量的乘积公式:
向量a=(x1,y1),向量b=(x2,y2)。
a·b=x1x2+y1y2=|a||b|cosθ(θ是a,b夹角)。
PS:向量之间不叫"乘积",而叫数量积。如a·b叫做a与b的数量积或a点乘b。
发展历史:
向量,最初被应用于物理学。很多物理量如力、速度、位移以及电场强度、磁感应强度等都是向量。大约公元前350年前,古希腊著名学者亚里士多德就知道了力可以表示成向量,两个力的组合作用可用著名的平行四边形法则来得到。
“向量”一词来自力学、解析几何中的有向线段。最先使用有向线段表示向量的是英国大科学家牛顿。
向量乘积怎么算
向量a乘以向量b=(向量a得模长)乘以(向量b的模长)乘以cosα[α为2个向量的夹角];向量a(x1,y1)向量b(x2,y2),向量a乘以向量b=(x1*x2,y1*y2)。
定义:向量a*b=绝对值里面的向量a*绝对值里面的向量b*cos(两个向量的夹角)=两个向量的模*两个向量夹角的余弦。
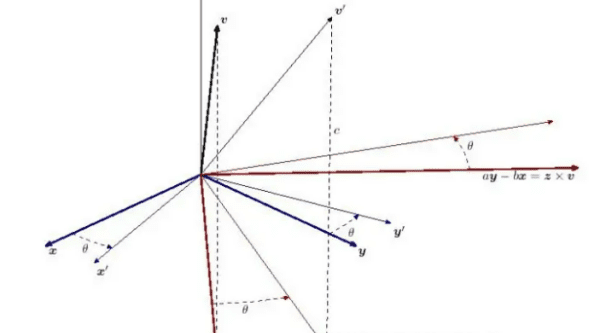
两个向量a和b的向量积(外积、叉积)是一个向量,记作a×b。若a、b不共线,则a×b的模是:∣a×b∣=|a|•|b|•sin〈a,b〉;a×b的方向是:垂直于a和b,且a、b和a×b按这个次序构成右手系。若a、b共线,则a×b=0。
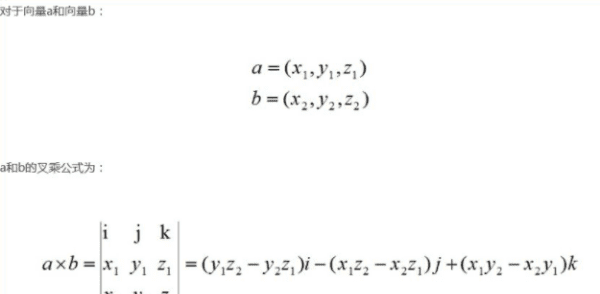
向量有关介绍:
向量的向量积性质:∣a×b∣是以a和b为边的平行四边形面积。a×a=0。a‖b〈=〉a×b=0。
向量的向量积运算律:a×b=-b×a;(λa)×b=λ(a×b)=a×(λb);(a+b)×c=a×c+b×c.注:向量没有除法,“向量AB/向量CD”是没有意义的。
向量的三角形不等式:∣∣a∣-∣b∣∣≤∣a+b∣≤∣a∣+∣b∣;①当且仅当a、b反向时,左边取等号;②当且仅当a、b同向时,右边取等号。∣∣a∣-∣b∣∣≤∣a-b∣≤∣a∣+∣b∣。①当且仅当a、b同向时,左边取等号;②当且仅当a、b反向时,右边取等号。
两个向量相乘如何计算
向量的乘法分为数量积和向量积两种。
对于向量的数量积,计算公式为:
A=(x1,y1,z1),B=(x2,y2,z2),A与B的数量积为x1x2+y1y2+z1z2。
对于向量的向量积,计算公式为:
A=(x1,y1,z1),B=(x2,y2,z2),则A与B的向量积为
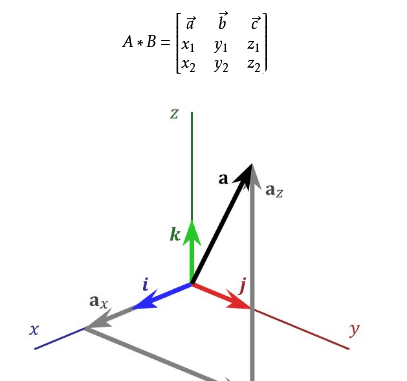
代数规则:
1、反交换律:a×b=-b×a
2、加法的分配律:a×(b+c)=a×b+a×c。
3、与标量乘法兼容:(ra)×b=a×(rb)=r(a×b)。
4、不满足结合律,但满足雅可比恒等式:a×(b×c)+b×(c×a)+c×(a×b)=0。
5、分配律,线性性和雅可比恒等式别表明:具有向量加法和叉积的R3构成了一个李代数。
6、两个非零向量a和b平行,当且仅当a×b=0。
以上就是关于向量积公式怎么算,两个向量的向量积怎么的全部内容,以及两个向量的向量积怎么求的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。