对称式方程怎么转化成一般式方程
对称式:(x-x0)/l=(y-y0)/m=(z-z0)/n转换成“交面式”,因所选用方程的不同可以有不同的形式,由“左方程”:(x-x0)/l=(y-y0)/m=>mx-mx0=ly-ly0=>mx-ly+ly0-mx0=0。
同理,由“右方程”ny-mz+mz0-ny0=0,则,经转换后交面式方程的各系数分别为:A1=m,B1=-l,C1=0,D1=ly0-mx0;A2=0,B2=n,C2=-m,D2=mz0-ny0。
如何将空间直线方程的对称式转换成一般式
对称式:(x-x0)/l=(y-y0)/m=(z-z0)/n 转换成“交面式”,因所选用方程的不同可以有不同的形式。
由“左方程”:(x-x0)/l=(y-y0)/m => mx-mx0=ly-ly0 => mx-ly+ly0-mx0=0
同理,由“右方程” ny-mz+mz0-ny0=0
则,经转换后交面式方程的各系数分别为:A1=m,B1=-l,C1=0,D1=ly0-mx0;A2=0,B2=n,C2=-m,D2=mz0-ny0
对称式如何化为一般式
举一个实例。把{2x+3y-4z+2=0 ;x+2y+3z-1=0 化为对称式 。
方法一:平面 2x+3y-4z+2=0 的法向量为 n1 =(2,3,-4),
平面 x+2y+3z-1=0 的法向量为 n2 =(1,2,3),
因此直线的方向向量为 v = n1×n2 =(17,-10,1)(向量叉乘会吧?)
取 x = 10,y = -6,z = 1 ,知直线过点 P(10,-6,1),
所以直线的对称式方程为 (x-10)/17 = (y+6)/(-10) = (z-1)/1 。
方法二:把 z 当已知数,可解得 x = 17z-7 ,y = 4-10z ,
由此得 (x+7)/17 = (y-4)/(-10) = z ,把最后的 z 改写成 (z-0)/1 ,就得结果。
方法三:取 z 的两个值如 z1 = 1 ,z2 = 2,
代入原方程可知直线过 A(10,-6,1),B(27,-16,2),
所以直线的方向向量为 AB =(27-10,-16+6,2-1)=(17,-10,1),
所以直线的方程为 (x-27)/17 = (y+16)/(-10) = (z-2)/1 。
扩展资料:
直线方程表达式:
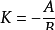
,
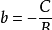
A1/A2=B1/B2≠C1/C2←→两直线平行
A1/A2=B1/B2=C1/C2←→两直线重合
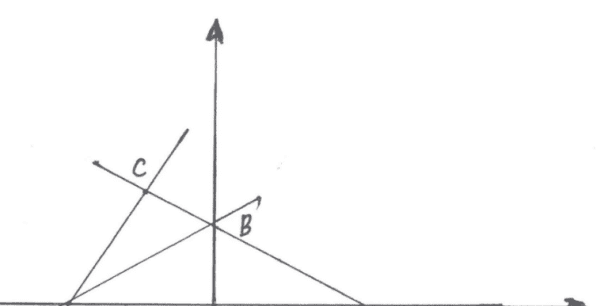
横截距a=-C/A
纵截距b=-C/B
2:点斜式:y-y0=k(x-x0) 【适用于不垂直于x轴的直线】
表示斜率为k,且过(x0,y0)的直线
3:截距式:x/a+y/b=1【适用于不过原点或不垂直于x轴、y轴的直线】
表示与x轴、y轴相交,且x轴截距为a,y轴截距为b的直线
4:斜截式:y=kx+b【适用于不垂直于x轴的直线】
表示斜率为k且y轴截距为b的直线
5:两点式:【适用于不垂直于x轴、y轴的直线】
表示过(x1,y1)和(x2,y2)的直线
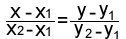
两点式
(y-y1)/(y2-y1)=(x-x1)/(x2-x1) (x1≠x2,y1≠y2)
6:交点式:f1(x,y) *m+f2(x,y)=0 【适用于任何直线】
表示过直线f1(x,y)=0与直线f2(x,y)=0的交点的直线
7:点平式:f(x,y) -f(x0,y0)=0【适用于任何直线】
表示过点(x0,y0)且与直线f(x,y)=0平行的直线
8:法线式:x·cosα+ysinα-p=0【适用于不平行于坐标轴的直线】
过原点向直线做一条的垂线段,该垂线段所在直线的倾斜角为α,p是该线段的长度
9:点向式:(x-x0)/u=(y-y0)/v (u≠0,v≠0)【适用于任何直线】
表示过点(x0,y0)且方向向量为(u,v )的直线
10:法向式:a(x-x0)+b(y-y0)=0【适用于任何直线】
表示过点(x0,y0)且与向量(a,b)垂直的直线。
以上就是关于对称式方程怎么转化成一般式方程的全部内容,以及对称式方程怎么转化成一般式方程的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。