人类为什么要计算圆周率，科学家为什么要计算圆周率

人类为什么要计算圆周率

因为计算圆周率在一定程度上可以反映出一个国家的科技水平；是精确计算圆周长、圆面积、球体积等几何形状的关键值。

圆周率是表示圆的周长与直径比值的数学常数，用希腊字母π表示。

π也等于圆形之面积与半径平方之比，近似值约等于3.14159265359。

科学家为什么要计算圆周率

1、数学证明:虽然圆周率已经被证明了是一个无限不循环的数字，但是科学却没有给过实践性的证明。如果能够一直研究下去，给理论一个实际的支持，那么这样的结果无疑是科学且严谨的。

2. 作为计算机的一种考验：圆周率的计算还可以作为检验计算机计算能力的一种手段。如果有两台电脑需要比赛计算能力，那就更好办了。同时启动两台电脑，开始计算，速度快慢一目了然。另外，圆周率的计算也是检验计算机性能的有效手段，这样可以检验出计算机是否出错，能不能借助圆周率编写程序，等等。所以，圆周率对于计算机来说，有着 特殊的存在意义。

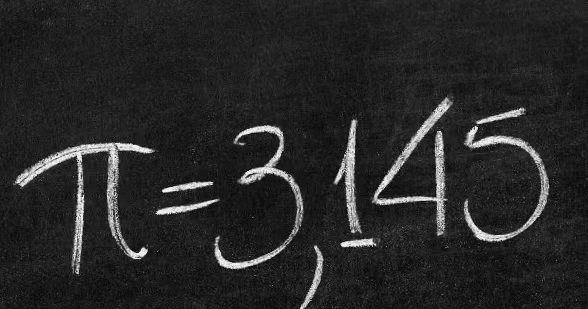
4、 验证科学：虽然结论已经给了我们圆周率是一个无限不循环的数字，但是不管是好奇心的驱使，还是本能的探索，都促使着人们想要去验证圆周率的最终结果。更有喜欢挑战的人，面对这一世界性的挑战，难免要跃跃欲试。

5、 对于世界有着特殊的意义：圆周率作为一个无限不循环的数字，世界中所有可能存在的数字组合，在圆周率都能够找到。所以，圆周率对于世界的意义是非凡的，上升到哲理，下降到记录，圆周率在我们的生活中其实还是有非常意义的。

圆周率的全文是什么

从现在的解释来看，圆周率是一个无限不循环的小数，现在人们已经把它计算到数十万亿位了。有很多人都觉得，圆周率对我们的生活，并没有太大作用，计算下去是没有意义的。实际上圆周率的应用，不仅仅是在数学上，像是天文学、航天学、生物学等，都有应用到圆周率的地方。另外还有一个问题，只要科学家能继续研究圆周率，他们就不会失去工作。

1、圆周率的应用问题对于普通人来说，圆周率就是用来计算圆周长和直径比值的，顶多就是一个公式，对自己没有任何影响。一直这样研究圆周率，貌似是没用的。实际上并不是如此，圆周率的计算很有意义，它并不是一个简单的数字，其中涉及到天文领域、航天领域、生物领域，可以说很多东西都跟它有关。有时候一个数字的错误，就有可能导致飞机无法起飞，飞船无法正常进入轨道。所以看似没有任何作用的圆周率，实际上是科研不可缺少的存在。

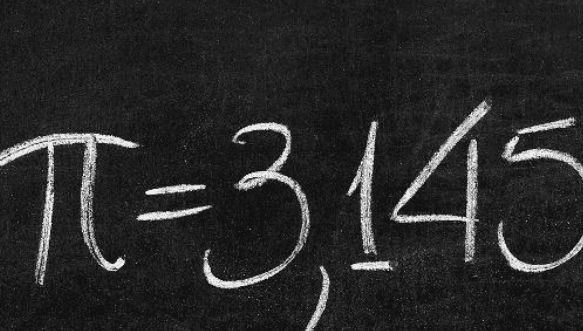
2、圆周率的验证圆周率是一个无限不循环的小数，它的关键点就在于不循环。很多人认为，世界上所有东西都是有规律的，没有东西可以逃出规律。研究圆周率，也是为了数字和科研的严谨性。现在计算机的计算能力，都是以万亿为单位的，如果科学家们发现了圆周率的最终结果，那么很有可能发现宇宙的奥秘。上到哲理下到运算，圆周率对生活有着非同一般的意义，这也是人们不停计算圆周率的理由。

3、为了不失业之前看到一个有趣的回答，说只要科学家们一直研究圆周率，就可以保证自己不失业。虽然听起来有点荒唐，但是还真有那么一点道理。当然这只是一个搞笑的解释，圆周率对于人们的意义重大，持续性的研究也是为了人类更好的发展。

人类为什么要研究圆周率

圆的周长与直径之比是一个常数，人们称之为圆周率．通常用希腊字母π来表示．1706年，英国人琼斯首创用π代表圆周率．他的符号并未立刻被采用，以后，欧拉予以提倡，才渐渐推广开来．现在π已成为圆周率的专用符号，π的研究，在一定程度上反映这个地区或时代的数学水平，它的历史是饶有趣味的．

圆周率

1600年，英国威廉·奥托兰特首先用π表示圆周率，因为π是希腊之“圆周”的第一个字母，而δ是“直径”的第一个字母，当δ=1时，圆周率为π．1706年英国的琼斯首先使用π．1737年欧拉在其著作中使用π．后来被数学家广泛接受，一直沿用至今．

英国的琼斯

π是一个非常重要的常数．一位德国数学家评论道：“历史上一个国家所算得的圆周率的准确程度，可以做为衡量这个国家当时数学发展水平的重要标志．”古今中外很多数学家都孜孜不倦地寻求过π值的计算方法．

在古代，实际上长期使用π＝3这个数值，巴比伦、印度、中国都是如此．到公元前2世纪，中国的《周髀算经》里已有“周三径一”的记载．东汉的数学家又将π值改为3.16．直正使圆周率计算建立在科学的基础上，首先应归功于阿基米德．他专门写了一篇论文《圆的度量》，用几何方法证明了圆周率与圆直径之比小于22/7而大于223/71．这是第一次在科学中创用上、下界来确定近似值．第一次用正确方法计算π值的，是魏晋时期的刘徽，在公元263年，他首创了用圆的内接正多边形的面积来逼近圆面积的方法，算得π值为3.14．我国称这种方法为割圆术．直到1200年后，西方人才找到了类似的方法．后人为纪念刘徽的贡献，将3.14称为徽率．

欧拉

公元460年，南朝的祖冲之利用刘徽的割圆术，把π值算到小点后第七位3.1415926，这个具有七位小数的圆周率在当时是世界首次．祖冲之还找到了两个分数：22/7和355/113，用分数来代替π，极大地简化了计算，这种思想比西方也早一千多年．可惜，祖冲之的计算方法后来失传了．人们推测他用了刘徽的割圆术,但究竟用什么方法，还是一个谜．

祖冲之

祖冲之出生在一个世代对天文历法都有所研究的家庭，受环境熏陶他自幼就对数学和天文学有着非常浓厚的兴趣．《宋书·律历志》中，祖冲之有这样的自述：“臣少锐愚，尚专攻数术，搜练古今，博采沈奥．后将夏典，莫不摸量，周正汉朔，咸加该验……此臣以俯信偏识，不虚推古人者也……”．由此可见，祖冲之从小时起便搜集、阅读了前人的大量数学文献，并对这些资料进行了深入系统的研究，坚持对每步计算都做亲身的考核验证，不被前人的成就所束缚，纠正其错误同时加之自己的理解与创造，使得他在以下三方面对我国古代数学有着巨大的推动：

一是圆周率的计算．他算得3.1415926＜π＜3.1415927且取为密率．π的取值范围及密率的计算都领先国外千余年．

二是球体积的计算．祖冲之与他的儿子祖恒一起找到了球体积的计算公式．这其中所用到的“祖恒原理”，“幂势既同则积不容异”，即等高处横截面积都相等的两个几何体的体积必相等．直到一千一百年后，意大利数学家卡瓦利里（B.Cavalieri）才提出与之有相仿意义的公理．

三是注解《九章算术》，并著《级术》、《级术》在唐代做为数学教育的课本，以“学官莫能究其深奥”而著称，可惜这部珍贵的典籍早已失传．

祖冲之在数学上的这些成就，使得这个时期在数学的某些方面“中国人不仅赶上了希腊人”，甚至领先他们一千年．

祖冲之的圆周率，保持了一千多年的世界记录．终于在1596年，由荷兰数学家卢道夫打破了．他把π值推到小数点后第15位小数，最后推到第35位．为了纪念他这项成就，人们在他1610年去世后的墓碑上，刻上3.14159265358979323846264338327950288这个数，从此也把它称为“卢道夫数”．

之后，西方数学家计算π的工作，有了飞速的进展．1948年1月，费格森与雷思奇合作，算出808位小数的π值．电子计算机问世后，π的人工计算宣告结束．20世纪50年代，人们借助计算机算得了10万位小数的π，70年代又突破这个记录，算到了150万位．到90年代初，用新的计算方法，算到的π值已到4.8亿位．π的计算经历了几千年的历史，它的每一次重大进步，都标志着技术和算法的革新．

以上就是关于人类为什么要计算圆周率，科学家为什么要计算圆周率的全部内容，以及人类为什么要计算圆周率的相关内容,希望能够帮到您。