用定积分的几何意义求积分
定积分几何意义是曲线与x=a、x=b、x轴所包围的面积的代数和(对x积分),求定积分需要给出积分函数、积分区间以及微元,而只给出了积分函数,没给出积分区间和微元。
定积分就是求函数f(X)在区间[a,b]中图线下包围的面积。即由y=0,x=a,x=b,y=f(X)所围成图形的面积。这个图形称为曲边梯形,特例是曲边三角形。
不定积分是一组导数相同的原函数,定积分则是一个数值。求一个函数的原函数,叫做求它的不定积分;求一个函数相应于闭区间的一个带标志点分划的黎曼和关于这个分划的参数趋于零时的极限,叫做这个函数在这个闭区间上的定积分。
利用定积分的几何意义求∫2xdx
解:定积分的几何意义是函数y=f(x)
的曲线,与其定义域的区间[a,b],即a≤x≤b所围成平面图形的面积。
本题中,f(x)=cosx,a=0,b=2π。
考察y=cosx在[0,2π]
的变化,利用y=cosx的对称性,可知y=cosx与x=0、x=2π所围成的平面图形的面积值为0,
故,∫(0,2π)cosxdx=0。
供参考。
利用定积分的几何意义求∫2xdx
(1)被积函数的曲线是圆心在原点,半径为2的半圆周,
由定积分的几何意义知此积分计算的是半圆的面积,
所以有
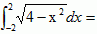
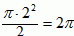
;
(2)∵被积函数为
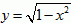
,其表示的曲线为以原点为圆心,1为半径的四分之一的圆,
由定积分的几何意义可知,所求的定积分即为该四分之一圆的面积,
∴
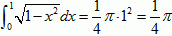
。
由定积分的几何意义计算定积分
根号下(1-x²)从-1到1的定积分,利用几何意义用圆面积公式直接求出。
被积函数与坐标轴围成的面积,x轴之上部分为正,x轴之下部分为负,根据cosx在[0,2π]区间的图像可知,正负面积相等,因此其代数和等于0。
定积分就是求函数f(X)在区间[a,b]中的图像包围的面积。即由y=0,x=a,x=b,y=f(X)所围成图形的面积,特例是曲边三角形。
扩展资料:
设f(x)区间[a,b]上有界,且只有有限个间断点,则f(x)在[a,b]上可积。设f(x)在区间[a,b]上单调,则f(x)在[a,b]上可积。
一个函数,可以存在不定积分,而不存在定积分;也可以存在定积分,而不存在不定积分。一个连续函数,一定存在定积分和不定积分;若只有有限个间断点,则定积分存在;若有跳跃间断点,则原函数一定不存在,即不定积分一定不存在。
定积分几何意义计算例题
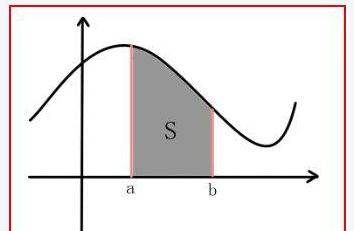
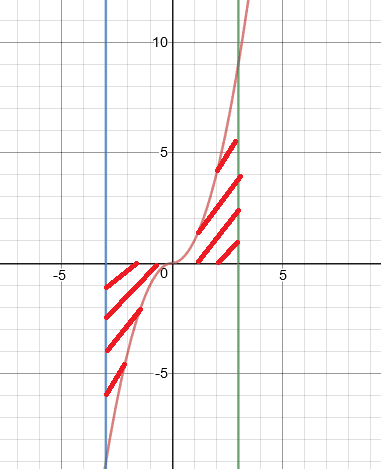
定积分的几何意义,就是被积函数与x轴围成的面积之和。如下图所示。
当被积函数为奇函数,y轴左侧的面积和y轴右侧的面积大小相等,符号相反,二者之和为0.
一般来说,奇函数在对称区间的定积分为0
因此:
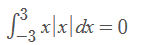
以上,请采纳。
以上就是关于用定积分的几何意义积分,利用定积分的几何意义求∫2xdx的全部内容,以及用定积分的几何意义求积分的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。