内切球的半径怎么求
求内切球的半径的有利用向量法、等体积法,等体积法就是类比等面积法,等面积法也叫等积法,两个三角形等底等高,则面积相等,因此两个三角形高相等,边成倍数关系。
如果一个球与简单多面体的各面或其延展部分都相切,且此球在多面体的内部,则称这个球为此多面体的内切球。
求正四面体内切球的半径
如下:
1、△ABC的三边分别为a、b、c,面积为S,内切圆半径为r,则:1/2ar+1/2br+1/2cr=S,r=2S/(a+b+c),这就是三角形中内切圆半径的计算公式,即三角形中内切圆半径等于面积的2倍除以周长。
四面体内切球半径公式:r=3V/(S1 S2 S3 S4)。球心到某几何体各面的距离相等且等于半径的球是几何体的内切球。如果一个球与简单多面体的各面或其延展部分都相切,且此球在多面体的内部,则称这个球为此多面体的内切球。
2、三棱锥锥体的一种,几何体,由四个三角形组成。固定底面时有一个顶点,不固定底面时有四个顶点。(正三棱锥不等同于正四面体,正四面体必须每个面都是正三角形)。
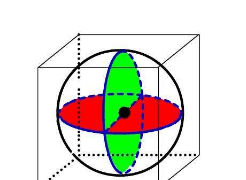
解决高中内切球问题的一般方法
抓住“接”和“切”的关键特征。
1、 外接球:外接球关键特征为外“接”。因此,各“接”点到球心距离相等且等于半径,解题时无论构造图形还是计算都要对此善加利用。
2、内切球:内切球关键特征为内“切”。因此,各“切”点到球心距离相等且等于半径,且与球心的连线垂直切面,解题时无论构造图形还是计算都要对此善加利用。
圆台内切球半径公式推导
呵呵,我在这里没法画图。你可以在稿纸上画出圆台的中截面图,是个梯形,再画出它的内切园,它的半径就是内切球的半径。可以连结两条圆心到梯形两个顶点的辅助线。可以证明这两条线和梯形斜边成直角三角形,圆半径就是斜边的高!设球半径为r,由:R1*R1+r*r+R2*R2+r*r=(R1+R2)*(R1+R2),解得:r=根号(R1*R2),由于不方便画图和有些符号不方便,只能这样了,谢谢!
正方体内切球外接球半径公式
无论从哪个角度看正八面体都可以看做上、下两个正方椎体黏合而成,外接圆可以看成与正方椎体底面正方形相切,假设正8面体边长为a,则外接圆半径为底面正方形对角线的一半=√2a/2;
内切的时候,正八面体的各个顶点A到圆心O的距离是相等的,作顶点到圆心的连线AO,则AO=√2a/2,AO与任何一个八面体的面线之间的夹角为30度,在八面体的任一面上作圆心O的投影O',则在直角三角形AOO'中OO'=√2a/4
正三棱锥内切球半径公式推导
正三棱锥内切球半径公式:V=R×S/3,三棱锥锥体的一种,几何体是由四个三角形组成,固定底面时有一个顶点,不固定底面时有四个顶点,正三棱锥不等同于正四面体,正四面体必须每个面都是正三角形。
三棱锥有四个面、四个顶点、六条棱、四个三面角、六个二面角与十二个面角。若四个顶点为A,B,C,D,则可记为四面体ABCD,当看做以A为顶点的三棱锥时,也可记为三棱锥A-BCD。
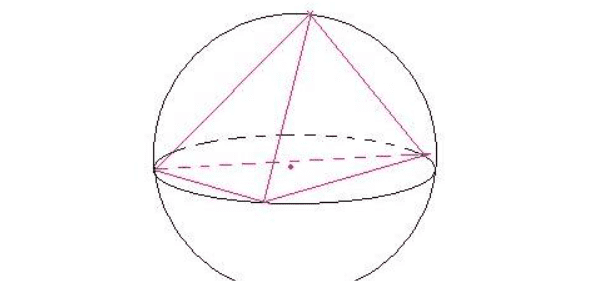
性质
1、底面是等边三角形。
2、侧面是三个全等的等腰三角形。
3、顶点在底面的射影是底面三角形的中心(也是重心、垂心、外心、内心)。
4. 常构造以下四个直角三角形:
(1)斜高、侧棱、底边的一半构成的直角三角形;(含侧棱与底边夹角)
(2)高、斜高、斜高射影构成的直角三角形;(含侧面与底面夹角)
(3)高、侧棱、侧棱射影构成的直角三角形;(含侧棱与底面夹角)
(4)斜高射影、侧棱射影、底边的一半构成的直角三角形。
以上就是关于内切球的半径怎么,求正四面体内切球的半径的全部内容,以及内切球的半径怎么求的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。