含有n个元素的集合有几个子集
有n个元素,每个元素都有取与不取的两种可能,所以应该是:2*2*.(n个)=2^n个子集。子集是一个数学概念,指某个集合中一部分的集合,亦称部分集合。
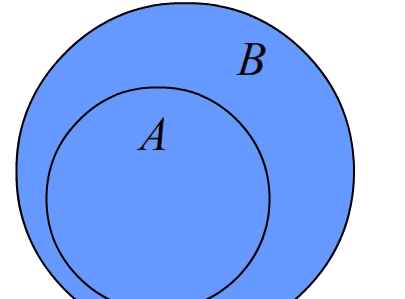
若A和B都为集合,且A中所有元素都是B中的元素,则A是B的子集或称A包含于B。符号语言:若?a∈A,均有a∈B,则A?B。
如果一个集合中有n个元素n表示子集
子集:2^N;非空子集:2^N-1;真子集:2^N-1 。
假设有实数x ①[x,y] :方括号表示包括边界,即表示x到y之间的数以及x和y; ②(x,y):小括号是不包括边界,即表示大于x、小于y的数。 有一类特殊的集合,它不包含任何元素,如{x|x∈R x²+1=0} ,称之为空集,记为∅。空集是个特殊的集合,它有2个特点: 1、空集∅是任意一个非空集合的真子集。 2、空集是任何一个集合的子集 。 扩展资料: 如果两个集合S和T的元素完全相同,则称S与T两个集合相等,记为S=T 。显然有如下关系: 其中符号 称为当且仅当,表示左边的命题与右边的命题相互蕴含,即两个命题等价。 有些集合可以用一些特殊符号表示,举例如下: N:非负整数集合或自然数集合{0,1,2,3,…} N*或N+:正整数集合{1,2,3,…} Z:整数集合{…,-1,0,1,…} Q:有理数集合 Q+:正有理数集合 Q-:负有理数集合 R:实数集合(包括有理数和无理数) R+:正实数集合 R-:负实数集合 C:复数集合 ∅ :空集(不含有任何元素的集合) 参考资料: 含有n个元素的集合共有2^n个子集! 2^n-1个真子集! 2^n-1个非空子集! 2^n-2个非空真子集! 采纳吧!!! n个元素的集合有2^n个子集。 子集介绍: 子集是一个数学概念:如果集合A的任意一个元素都是集合B的元素,那么集合A称为集合B的子集。符号语言:若∀a∈A,均有a∈B,则A⊆B。 性质: 命题1:空集是任意集合的子集。 证明:给定任意集合A,要证明Φ是A的子集。这要求给出所有Φ的元素是A的元素;但是,Φ没有元素。 对有经验的数学家们来说,推论Φ没有元素,所以Φ的所有元素是A的元素是显然的;但对初学者来说,有些麻烦。因为Φ没有任何元素,如何使"这些元素"成为别的集合的元素?换一种思维将有所帮助。 为了证明Φ不是A的子集,必须找到一个元素,属于Φ,但不属于A。因为Φ没有元素,所以这是不可能的。因此Φ一定是A的子集。这个命题说明:包含是一种偏序关系。 命题2:若A,B,C是集合,则: 自反性:A⊆A;反对称性:A⊆B且B⊆A,当且仅当A=B;传递性:若A⊆B且B⊆C则A⊆C。这个命题说明:对任意集合S,S的幂集按包含排序是一个有界格,与上述命题相结合,则它是一个布尔代数。 命题3:若A,B,C是集合S的子集,则: 存在一个最小元和一个最大元:Φ⊆A⊆S(thatΦ⊆A is Proposition 1 above.);存在并运算:A⊆A∪B;若A⊆C且B⊆C则A∪B⊆C;存在交运算:A∩B⊆A;若C⊆A且C⊆B则C⊆A∩B。 这个命题说明:表述"A⊆B"和其他使用并集,交集和补集的表述是等价的,即包含关系在公理体系中是多余的。 共2的n次方个子集。 如果集合A的任意一个元素都是集合B的元素(任意a∈A则a∈B),那么集合A称为集合B的子集,记为A⊆B或 B⊇A,读作“集合A包含于集合B”或集合B包含集合A”。 即:∀a∈A有a∈B,则A⊆B。 性质 一、根据子集的定义,我们知道A⊆A。也就是说,任何一个集合是它本身的子集。 二、对于空集∅,我们规定∅⊆A,即空集是任何集合的子集。 说明:若A=∅,则∅⊆A仍成立。 证明:给定任意集合A,要证明∅是A的子集。这要求给出所有∅的元素是A的元素;但是,∅没有元素。对有经验的数学家们来说,推论“∅没有元素,所以∅的所有元素是A 的元素"是显然的;但对初学者来说,有些麻烦。 因为∅没有任何元素,如何使"这些元素"成为别的集合的元素? 换一种思维将有所帮助。 以上就是关于含有n个元素的集合有几个子集的全部内容,以及含有n个元素的集合有几个子集的相关内容,希望能够帮到您。 版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。
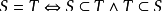

包含n个元素的集合有多少个子集
n个元素的集合有几个子集,真子集和非空真字集


一个集合有n个元素有多少个子集证明