置信椭圆是什么
置信椭圆基本上是对置信区域的描述方式,其长轴和短轴分别为置信区域的参数,置信椭圆的长短半轴,分别表示二维位置坐标分量的标准差(如经度的σλ和纬度的σφ)。
一倍标准差(1σ)的概率值是68.3%,二倍标准差(2σ)的概率值为95.5%;三倍标准差(3σ)的概率值是99.7%。
散点图加置信椭圆
在使用SIMCA(Soft Independent Modeling of Class Analogy)进行主成分分析(PCA)并绘制PCA图时,可以通过添加置信椭圆来显示类别之间的显著差异。
下面是如何在SIMCA作PCA图中添加置信椭圆的步骤:首先,在SIMCA建模时,需要选择“Compute classification statistics”选项。这将生成一个结果表,其中包含类别的均值向量、协方差矩阵和误差边界。接下来,通过绘制PCA图来显示数据的主要方差方向。在绘制PCA图时,可以选择将类别标记为不同的颜色和/或符号。在绘制PCA图之后,可以通过在类别均值点周围绘制椭圆来显示误差边界。椭圆的大小和方向与协方差矩阵有关。在SIMCA软件中,可以通过选择“Add confidence ellipse”选项来添加置信椭圆。该选项将打开一个对话框,其中可以选择要添加置信椭圆的类别以及椭圆的样式和颜色。最后,确认所选的选项并绘制PCA图。现在,每个类别的均值点周围都会有一个椭圆,表示该类别的误差边界。注意,置信椭圆并不代表所有的类别都有相同的误差边界,因此需要仔细解释椭圆的含义和限制。
线性代数在计算机学科上到底有什么应用
线性代数在计算机学科上的应用:
计算机数学基础是计算机专业必修的数学基础知识,针对计算机专业的特点,加强了Mathematica数学软件的应用。包含4大模块:微积分、线性代数、概率论。
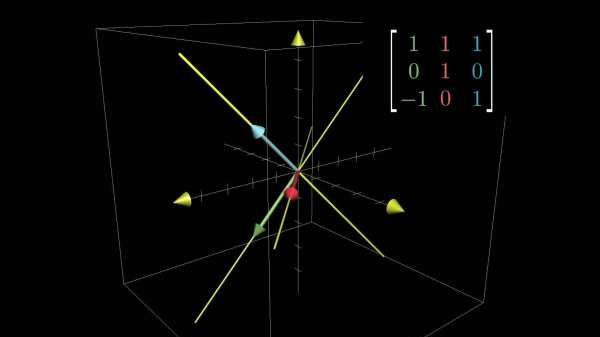
计算机图形学、计算机辅助设计、密码学、虚拟现实等技术无不以线性代数为其理论和算法基础的一部分。
随着科学的发展,不仅要研究单个变量之间的关系,还要进一步研究多个变量之间的关系,各种实际问题在大多数情况下可以线性化,而由于计算机的发展,线性化的问题又可以被计算出来,线性代数正是解决这些问题的有力工具。
扩展资料:
线性代数的应用:
1、线性代数的理论和方法已经渗透到数学的许多分支,同时也是理论物理和理论化学所不可缺少的代数基础知识。
2、线性代数在工程技术和国民经济的许多领域都有着广泛的应用,是一门基本的和重要的学科。
3、线性是人类少数可以研究得非常透彻的数学基础性框架。
pca置信椭圆怎么看
在SIMCA中,要在PCA图中添加置信椭圆,可以按照以下步骤操作:
打开SIMCA软件并载入数据,进行PCA分析。
在PCA图窗口中,选择“Scores”或“Loadings”选项卡,分别查看得分图或载荷图。
在“Scores”或“Loadings”选项卡上方的工具栏中,找到“Ellipse”图标,点击打开“Ellipse Setup”窗口。
在“Ellipse Setup”窗口中,选择需要添加置信椭圆的分组,可以选择“Groups”中已有的分组,也可以创建新的分组。
在“Ellipse Setup”窗口中,设置置信椭圆的参数,包括置信水平、椭圆线条颜色、线条宽度等等。
点击“Apply”或“OK”按钮,保存设置并关闭“Ellipse Setup”窗口。
在PCA图窗口中,可以看到添加了置信椭圆的得分图或载荷图。
需要注意的是,添加置信椭圆需要保证数据已经进行标准化处理,并且需要有已知的类别信息,才能将样本分组并在不同组之间绘制置信椭圆。
以上就是关于置信椭圆是什么,散点图加置信椭圆的全部内容,以及置信椭圆是什么的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。


