共轭复数怎么求
共轭复数,两个实部相等,虚部互为相反数的内复数互为共轭复数)。
当虚部不为零时,共轭复数就是实部相等,虚部相反,如果虚部为零,其共轭复数就是自身(当虚部不等于0时也叫共轭虚数)。
复数z的共轭复数记作z(上加一横),有时也可表示为Z*。
同时,复数z(上加一横)称为复数z的复共轭。
根据定义,若z=a+bi(a,b∈R),则z=a-bi(a,b∈R)。
两个复数:x+yi与x-yi称为共轭复数,它度们的实部相等,虚部互为相反数。
在复平面上,表示两个共轭复数的点关于X轴对称,而问这一点正是"共轭"一词的来源。
两头牛平行地拉一部犁,它们的肩膀上要共架一个横梁,这横梁就叫做"轭"。
如果用z表示x+yi,那么在z字上面答加个"一"就表示x-yi,或相反。
共轭复数怎么求
复数的共轭复数很简单,只要把虚部取反即可,例如:复数5/3+4i的共轭复数是5/3-4i。
当两个复数实部相等,虚部互为相反数时,这两个复数互为共轭复数,其几何特征是复平面上关于实轴对称的点,即复数z=a+bi(a,b∈R)的共轭复数为 (a,b∈R)。

共轭复数的性质
(1)︱x+yi︱=︱x-yi︱;
(2)(x+yi)*(x-yi)=x2+y2=︱x+yi︱2=︱x-yi︱2。
如果两个复数相等a+bi=c+di, 移项后得到a+bi-(c+di)=0, 根据复数的减法有(a-c)+(b-d)i=0. 复数等于零, 只有实部和虚部都为零, 于是得到a=c, b=d. 因此两个复数相等意味着实部与实部相等, 虚部与虚部相等。
共轭复数怎么求
解答过程如下:
y²-2y+10=0
根据一元二次方程根的公式,有:
y=[-(-2)±√(-2)²-4×1×10]/2=(2±√-36)/2=(2±√36i²)/2=1±6i
扩展资料:
共轭复数
两个实部相等,虚部互为相反数的复数互为共轭复数(conjugate complex number)。(当虚部不等于0时也叫共轭虚数)复数z的共轭复数记作
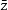
(z上加一横,英文中可读作Conjugate z,z conjugate or z bar),有时也可表示为
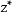
。
根据定义,若z=a+ib(a,b∈R),则
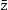
=a-ib(a,b∈R)。在复平面上,共轭复数所对应的点关于实轴对称。(如右图)
共轭根式
当
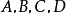
都是有理根式,而
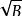
、
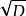
中至少有一个是无理根式时,称
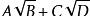
和
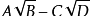
互为“共轭根式”。由平方差公式,这两式的积为有理式
共轭双曲线
以已知双曲线的虚轴为实轴,实轴为虚轴的双曲线叫做原双曲线的共轭双曲线,如双曲线H:
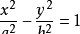
与 双曲线H':
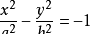
叫做一对共轭双曲线(a>0,b>0)。
主要性质有:它们有共同的渐近线,它们的四个焦点共圆,它们的离心率的倒数的平方和等于1。
共轭复数的概念及运算
1.
基本概念:共轭复数,两个实部相等,虚部互为相反数的复数互为共轭复数。当虚部不为零时,共轭复数就是实部相等,虚部相反,如果虚部为零,其共轭复数就是自身。
2.
运算方法:
(1)加法法则:设z1=a+bi,z2=c+di是任意两个复数。两者和的实部是原来两个复数实部的和,它的虚部是原来两个虚部的和。两个复数的和依然是复数。即
(a+bi)±(c+di)=(a±c)+(b±d)i.
(2)减法法则:两个复数的差为实数之差加上虚数之差(乘以i),即:z1-z2=(a+ib)-(c+id)=(a-c)+(b-d)i。
(3)乘法法则:把两个复数相乘,类似两个多项式相乘,结果中i^2
=
-1,把实部与虚部分别合并。两个复数的积仍然是一个复数。
(4)除法法则:满足(c+di)(x+yi)=(a+bi)的复数x+yi(x,y∈R)叫复数a+bi除以复数c+di的商运算方法:将分子和分母同时乘以分母的共轭复数,再用乘法法则运算。
(5)开放法则:若z^n=r(cosθ+isinθ),则z=n√r[cos(2kπ+θ)/n+isin(2kπ+θ)/n](k=0,1,2,3……n-1)
运算特征:
(1)(z1+z2)′=z1′+z2′
(2)
(z1-z2)′=z1′-z2′
(3)
(z1·z2)′=z1′·z2′
(4)
(z1/z2)′=z1′/z2′
(z2≠0)
总结:和(差、积、商)的共轭等于共轭的和(差、积、商)。
以上就是关于共轭复数怎么的全部内容,以及共轭复数怎么求的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。