什么样的函数具有反函数
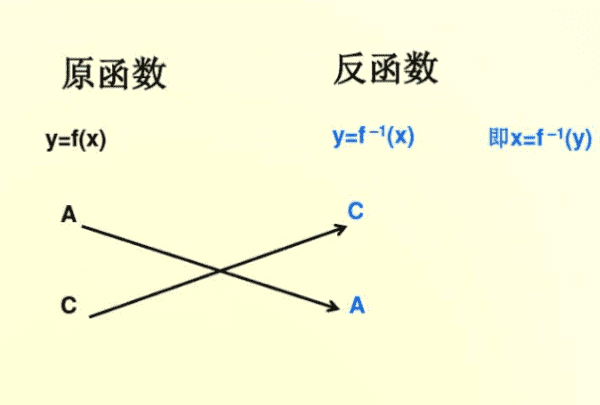
反函数y=f-1(x)的定义域、值域分别是函数y=f(x)的值域、定义域,最具有代表性的反函数就是对数函数与指数函数,存在反函数的条件是原函数必须是一一对应的,一函数f若要是反函数就必须是一双射函数。
偶函数必然没有反函数,因为偶函数满足f(x)=f(-x)。
函数有反函数的充要条件
例子:y=2x,反函数是x=y/2。
由y=2x得dy/dx=2,由x=y/2得dx/dy=1/2;显然二者互为倒数。
反函数的性质:
1、函数f(x)与它的反函数f-1(x)图象关于直线y=x对称。
2、函数存在反函数的充要条件是,函数的定义域与值域是一一映射。
3、一个函数与它的反函数在相应区间上单调性一致。
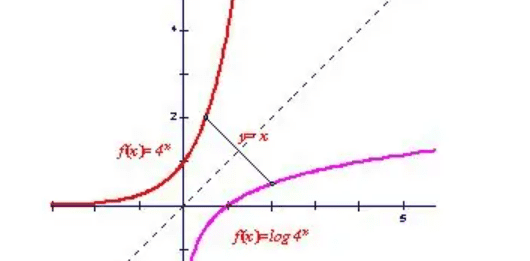
反函数存在定理
定理:严格单调函数必定有严格单调的反函数,并且二者单调性相同。在证明这个定理之前先介绍函数的严格单调性。
设y=f(x)的定义域为D,值域为f(D)。如果对D中任意两点x1和x2,当x1
什么样的函数具有反函数的定义
在定义域内单调的函数具有反函数
在定义域内单调的函数具有反函数。反函数y=f-1(x)的定义域、值域分别是函数y=f(x)的值域、定义域,最具有代表性的反函数就是对数函数与指数函数,存在反函数的条件是原函数必须是一一对应的,一函数f若要是反函数就必须是一双射函数。偶函数必然没有反函数,因为偶函数满足f(x)=f(-x)。
原函数值域就是反函数定义域,而原函数定义域则是反函数值域,它们在各自的定义域上单调性也一样。对于函数而言,它的反函数本也是一个函数,根据反函数的定义,可以得出原函数是其反函数的反函数,所以对于函数而言,原函数和反函数互相称为反函数。
反函数与原函数的关系
1、反函数的定义域是原函数的值域,反函数的值域是原函数的定义域。
2、互为反函数的两个函数的图像关于直线y=x对称。
3、原函数若是奇函数,则其反函数为奇函数。
4、若函数是单调函数,则一定有反函数,且反函数的单调性与原函数的一致。
5、原函数与反函数的图像若有交点,则交点一定在直线y=x上或关于直线y=x对称出现。
函数的作用和表达式语法
sum函数
sum函数即求和函数,主要用来计算两个或多个值,或者单元格区域的求和计算,最常用于一个单元格区域的求和计算,但在复杂的组合函数中,也使用频繁,比如与offset、small等函数的组合应用。
if函数
if函数我们也俗称判断函数,作用是判断一个条件是否为真,如果为真会返回一个值,否则会返回另一个值。
if和sum函数是公认的基础函数,常用函数,但if函数的作用其实远不止表面上的一点,通过各种嵌套,可以完成很多复杂的工作。
因此if函数也流传出万金油的称号。
lookup函数
lookup函数用于查找一行或列的值并返回另一行或列对应的值,简单而言,就是查询匹配,比如查询某个文本在A列的位置,然后匹配它在B列对应的位置。
在vlookup函数没出来之前,lookup函数可谓实用之极,现在也相当常用,如分数区间的匹配,业绩提成的分配等。
此外lookup函数有两种不同的表达式语法,其作用也不尽相同。
什么样的函数存在反函数
反函数转换的方法如下:
1、通过求出,即根据以x为自变量的原函数表达式转换成以y为自变量的函数表达式。

2、将新的表达式中,x和y互换位置,就得到反函数的表达式。
3、求定义域,反函数的定义域就是原来函数的值域。
反函数的性质:
1、函数存在反函数的充要条件是,函数的定义域与值域是一一映射。
2、一个函数与它的反函数在相应区间上单调性一致。
3、大部分偶函数不存在反函数。奇函数不一定存在反函数,被与y轴垂直的直线截止能过2个及以上点即没有反函数。若一个奇函数存在反函数,则它的反函数也是奇函数。
4、一组连续的函数的单调性在对应区间内具有一致性。
5、严增(减)的函数一定有严格增(减)的反函数。
6、反函数是相互的且具有唯一性。
7、定义域、值域相反对应法则互逆(三反)。
什么样的函数有反函数但不单调
只有单调函数才有反函数
以上就是关于什么样的函数具有反函数,函数有反函数的充要条件的全部内容,以及什么样的函数具有反函数的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。