如何用定积分的几何意义求定积分
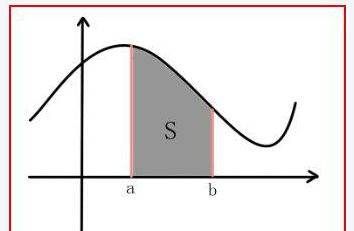
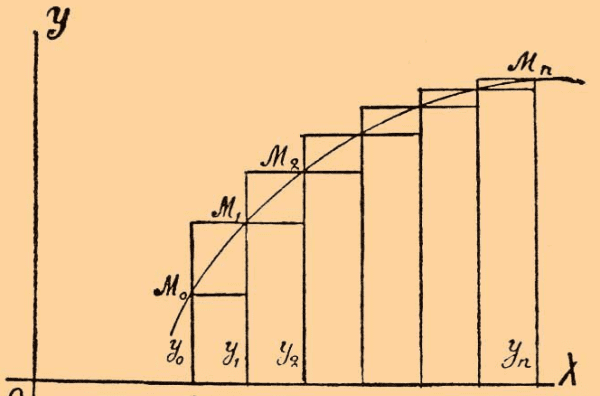
定积分的几何定义:可以理解为在Oxy坐标平面上,由曲线y=f(x)与直线x=a,x=b以及x轴围成的曲边梯形的度面积值(一种确定的实数值),也就是被积函数与x轴围成的面积之和。
利用定积分的几何意义求定积分的解法突破在于:一般情况下,定积分f(x)dx的值的几何意义是介于x轴、函数f(x)的图像以及直线x=a,x=b之间各部分面积的代数和,在x轴上方的积分值取正号,在x轴下方的积分值取负号。
由定积分的几何意义计算定积分
根号下(1-x²)从-1到1的定积分,利用几何意义用圆面积公式直接求出。
被积函数与坐标轴围成的面积,x轴之上部分为正,x轴之下部分为负,根据cosx在[0,2π]区间的图像可知,正负面积相等,因此其代数和等于0。
定积分就是求函数f(X)在区间[a,b]中的图像包围的面积。即由y=0,x=a,x=b,y=f(X)所围成图形的面积,特例是曲边三角形。
扩展资料:
设f(x)区间[a,b]上有界,且只有有限个间断点,则f(x)在[a,b]上可积。设f(x)在区间[a,b]上单调,则f(x)在[a,b]上可积。
一个函数,可以存在不定积分,而不存在定积分;也可以存在定积分,而不存在不定积分。一个连续函数,一定存在定积分和不定积分;若只有有限个间断点,则定积分存在;若有跳跃间断点,则原函数一定不存在,即不定积分一定不存在。
利用定积分的几何意义计算
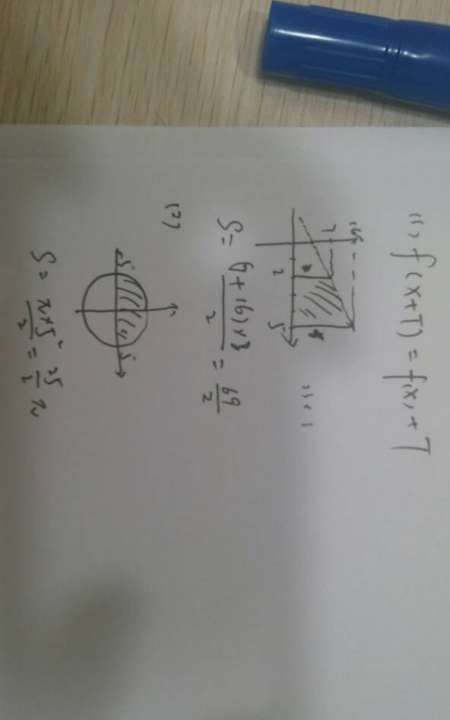
定积分几何意义计算例题
定积分的几何意义,就是被积函数与x轴围成的面积之和。如下图所示。
当被积函数为奇函数,y轴左侧的面积和y轴右侧的面积大小相等,符号相反,二者之和为0.
一般来说,奇函数在对称区间的定积分为0
因此:
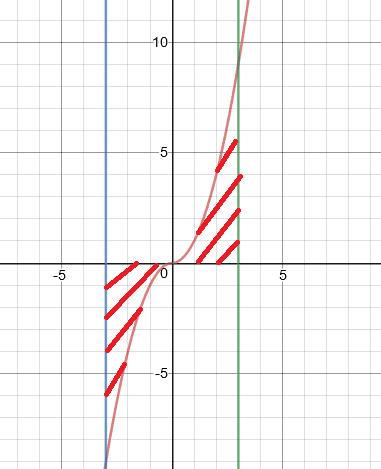
以上,请采纳。
利用定积分的几何意义求∫2xdx
定积分是积分的一种,是函数f(x)在区间[a,b]上的积分和的极限。注意定积分与不定积分之间的关系:若定积分存在,则它是一个具体的数值(曲边梯形的面积),而不定积分是一个函数表达式,它们仅仅在数学上有一个计算关系(牛顿-莱布尼茨公式)。
扩展资料:
定积分定义:
设函数f(x) 在区间[a,b]上连续,将区间[a,b]分成n个子区间[x0,x1], (x1,x2], (x2,x3], …, (xn-1,xn],其中x0=a,xn=b。可知各区间的长度依次是:△x1=x1-x0,在每个子区间(xi-1,xi]中任取一点ξi(1,2,...,n),作和式
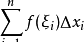
。该和式叫做积分和,设λ=max{△x1, △x2, …, △xn}(即λ是最大的区间长度),如果当λ→0时,积分和的极限存在,则这个极限叫做函数f(x) 在区间[a,b]的定积分,记为
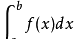
,并称函数f(x)在区间[a,b]上可积。 [2] 其中:a叫做积分下限,b叫做积分上限,区间[a, b]叫做积分区间,函数f(x)叫做被积函数,x叫做积分变量,f(x)dx 叫做被积表达式,∫ 叫做积分号。之所以称其为定积分,是因为它积分后得出的值是确定的,是一个常数, 而不是一个函数。根据上述定义,若函数f(x)在区间[a,b]上可积分,则有n等分的特殊分法:
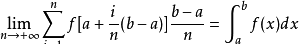
特别注意,根据上述表达式有,当[a,b]区间恰好为[0,1]区间时,则[0,1]区间积分表达式为:
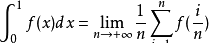
参考资料:
以上就是关于如何用定积分的几何意义定积分,由定积分的几何意义计算定积分的全部内容,以及如何用定积分的几何意义求定积分的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。