导数的物理意义和几何意义
导数的几何意义是该函数曲线在这一点上的切线斜率。导数的物理意义:导数物理意义随不同物理量而不同,但都是该量的变化的快慢函数,既该量的变化率,是函数的切线。如位移对求导就是速度,速度求导就是加速度,对功求导就是功的改变率等等。
导数(Derivative)是微积分中的重要基础概念。当自变量的增量趋于零时,因变量的增量与自变量的增量之商的极限。一个函数存在导数时,称这个函数可导或者可微分。可导的函数一定连续。不连续的函数一定不可导。导数实质上就是一个求极限的过程,导数的四则运算法则来源于极限的四则运算法则。
二阶导数的物理意义是什么
导数的数学意义是:函数y=f(x)在x0点的导数f'(x0)的几何意义:表示函数曲线在点P0(x0,f(x0))处的切线的斜率(导数的几何意义是该函数曲线在这一点上的切线斜率)。
导数的物理意义是:导数可以表示运动物体的瞬时速度和加速度(就直线运动而言,位移关于时间的一阶导数是瞬时速度,二阶导数是加速度),可以表示曲线在一点的斜率,还可以表示经济学中的边际和弹性。
导数与物理,几何,代数关系密切:在几何中可求切线;在代数中可求瞬时变化率;在物理中可求速度、加速度。
导数亦名纪数、微商(微分中的概念),是由速度变化问题和曲线的切线问题(矢量速度的方向)而抽象出来的数学概念,又称变化率。

扩展资料
发展:
1、前苏联
前苏联著名数学大师舍盖·索伯列夫为了确定偏微分方程解的存在性和唯一性,建立了广义函数和广义导数的概念。这一概念的引入不仅赋予微分方程的解以新的含义,更重要的是,它使得泛函分析等数学工具得以应用到微分方程理论中,从而开辟了微分方程理论的新天地。
2、美国
美籍华裔数学大师陈省身所研究的微分几何领域,便是利用微积分的理论来研究几何,这门学科对人类认识时间和空间的性质发挥着巨大的作用,并且这门学科至今仍然很活跃。前不久由俄罗斯数学家佩雷尔曼完成的庞加莱猜想便属于这一领域 。
3、中国
中国的数学爱好者发现了积乘和微商,使微积分的内容进一步拓展。
导数的意义是什么意思
物理意义:经常表示瞬间的变化率,在物理量中最常用的有瞬时速度和瞬时加速度。导数的几何意义:表示曲线在点处的切线的斜率。导数的本质是通过极限的概念对函数进行局部的线性逼近。
当函数y=f(x)的自变量x在一点x0上产生一个增量Δx时,函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在,a即为在x0处的导数,记作f'(x0)或df(x0)/dx。
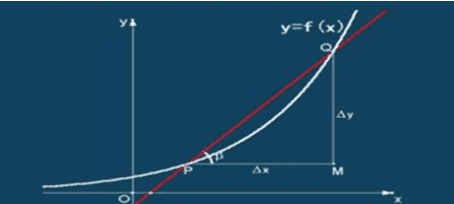
导数与函数的性质:
1、单调性
(1)若导数大于零,则单调递增;若导数小于零,则单调递减;导数等于零为函数驻点,不一定为极值点。需代入驻点左右两边的数值求导数正负判断单调性。
(2)若已知函数为递增函数,则导数大于等于零;若已知函数为递减函数,则导数小于等于零。
2、凹凸性
可导函数的凹凸性与其导数的单调性有关。如果函数的导函数在某个区间上单调递增,那么这个区间上函数是向下凹的,反之则是向上凸的。
如果二阶导函数存在,也可以用它的正负性判断,如果在某个区间上恒大于零,则这个区间上函数是向下凹的,反之这个区间上函数是向上凸的。曲线的凹凸分界点称为曲线的拐点。
什么是导数
导数的概念与几何意义
1. 导数的概念
设函数 在 及其近旁有定义,用 表示 的改变量,于是对应的函数值改变量为 ,如果极限 存在极限,则称函数 在点 处可导,此极限值叫函数 在点 处的导数,记作 或
称为函数 在 到 之间的平均变化率,函数 在点 处的导数即平均变化率当 时的极限值。
2. 导数的几何意义
函数 在一点 的导数等于函数图形上对应点 的切线斜率,即 ,其中 是过 的切线的倾斜角,过点 的切线方程为
3. 导数的物理意义
函数 在 的导数是函数在该点处平均变化率的极限,即瞬时变化率,若函数 表示运动路程,则 表示在 时刻的瞬时速度。
4. 导函数的概念
如果函数 在开区间 内每一点都可导,就说 在 内可导,这时,对于开区间 内每个确定的值 都对应一个确定的导数 ,这就在 内构成一个新的函数,此函数就称为 在 内的导函数,记作 或 ,即
而当 取定某一数值 时的导数是上述导函数的一个函数值。
导数与导函数概念不同,导数是在一点处的导数 ,导函数是某一区间 内的导数,对
导函数是以 内任一点 为自变量,以 处的导数值为函数值的函数关系,导函数反映的是一般规律,而 等于某一数值时的导数是此规律中的特殊性。
以上就是关于导数的物理意义和几何意义,二阶导数的物理意义是什么的全部内容,以及导数的物理意义和几何意义的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。