如何用定义求函数在某一点的导数
首先判断函数在这个点x0是否有定义,即f(x0)是否存在;其次判断f(x0)是否连续,即f(x0-),f(x0+),f(x0)三者是否相等;再次判断函数在x0的左右导数是否存在且相等,即f‘(x0-)=f“(x0+),只有以上都满足了,则函数在x0处才可导。
函数(function)的定义通常分为传统定义和近代定义,函数的两个定义本质是相同的,只是叙述概念的出发点不同,传统定义是从运动变化的观点出发,而近代定义是从集合、映射的观点出发。函数的近代定义是给定一个数集A,假设其中的元素为x,对A中的元素x施加对应法则f,记作f(x),得到另一数集B,假设B中的元素为y,则y与x之间的等量关系可以用y=f(x)表示,函数概念含有三个要素:定义域A、值域C和对应法则f。其中核心是对应法则f,它是函数关系的本质特征。
用导数的定义求极限的方法
根据导数的定义,第一步求函数的增量△y,第二步求平均变化率
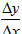
,第三步取极限得导数,
∵
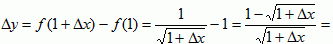
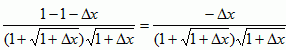
∴
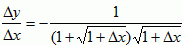
∴f′(1)=
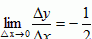
。
函数在一处连续说明什么
先去掉绝对值号,表示成分段函数后求导,分界点处利用导数的定义求导。
求导是数学计算中的一个计算方法,它的定义就是,当自变量的增量趋于零时,因变量的增量与自变量的增量之商的极限。
在一个函数存在导数时,称这个函数可导或者可微分。 可导的函数一定连续。 不连续的函数一定不可导。
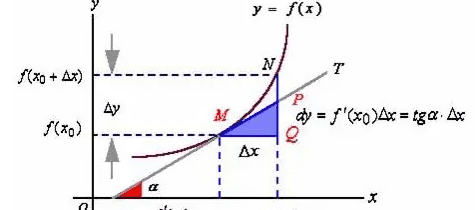
求导注意:
理解可导函数的单调性与其导数的关系;了解可导函数在某点取得极值的必要条件和充分条件(导数在极值点两侧异号);会求一些实际问题(一般指单峰函数)的最大值和最小值。解导数概念的某些实际背景(如瞬时速度、加速度、光滑曲线切线的斜率等);掌握函数在一点处的导数的定义和导数的几何意义;理解导数的概念。
如果函数在某点连续,那么在该点的导数一定存在
两种方法:
1、先求出函数的导函数,再把这点代入导函数即可
2、用定义求即 f`(x0)=lin(x→x0)[f(x)-f(x0)]/(x-x0)
函数在某点处的导数怎么求
首先,概念上有个问题
狄利克雷函数D(x)
x为有理数时 D(x)= 1
x为无理数时D(x)= 0
这个函数能帮你辨析一些模糊的概念。构造函数 f(x)= x²D(x) 你可以明显发现。这个函数,除了在x=0处可导连续外,在其他x=0邻域内都不连续。
楼主你遇到的这类题,往往要采用导数定义式去算,洛必达要用,要在x=x0的邻域里用。一点可导,无法使用洛必达,但是,一点可导,却可以用导数定义式来算。凑导数定义式,然后再算,才是正确的解题步骤。
以上就是关于用导数的定义求极限的方法,如何用定义函数在某一点的导数的全部内容,以及如何用定义求函数在某一点的导数的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。