3的x次方的导数怎么求
3的x次方的导数的求法:由导数公式y=a^x,y“=a^xlna,所以3^x的导数等于3^xln3。
导数也叫导函数值,又名微商,是微积分中的重要基础概念。
当函数y=f(x)的自变量x在一点x0上产生一个增量Δx时,函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在,a即为在x0处的导数,记作f“(x0)或df(x0)/dx。
三的x次方的导数是多少
3的x次方的导数的求法:由导数公式y=a^x,y'=a^xIna,所以3^x的导数等于3^xIn3。
扩展
导数也叫导函数值,又名微商,是微积分中的重要基础概念。当函数y=f(x)的自变量x在一点x0上产生一个增量Δx时,函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在,a即为在x0处的导数,记作f'(x0)或df(x0)/dx。
数学历史
数学是一门历史悠久、发展迅速的学科,其发展历程见证了人类智慧和文明的演变。

早在公元前4000年左右,人类就开始使用简单的计数系统,例如古埃及人和古巴比伦人使用的10进位系统。这些系统虽然简单,但却为后来的数学发展奠定了基础。在古希腊时期,数学开始成为一门独立的学科。
当时,毕达哥拉斯、欧几里得等数学家开始研究几何学、代数学和数论等领域,成为了古代数学的代表。
毕达哥拉斯定理是古希腊几何学中最著名的定理之一,它表明在一个直角三角形中,斜边的平方等于另外两条边的平方和。

欧几里得的《几何原本》是古希腊几何学中的经典著作,它讨论了几何学的基本概念和定理,对后来的数学发展产生了深远的影响。另外,数学家阿基米德在几何学和物理学方面也做出了重要的贡献。
在古印度和中国,数学也得到了独立的发展。古印度数学家阿耶尔巴塔在代数学和三角学领域有着很高的成就。中国的古代数学以算术和代数学为主,其中算盘是古代计算工具的代表,古代中国数学家刘徽的《九章算术》是古代中国数学的经典著作之一。
y=3^x的导数是多少
您好,很荣幸为您解答。
由公式
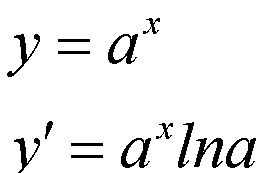
得:
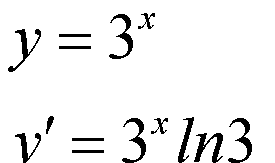
如图:
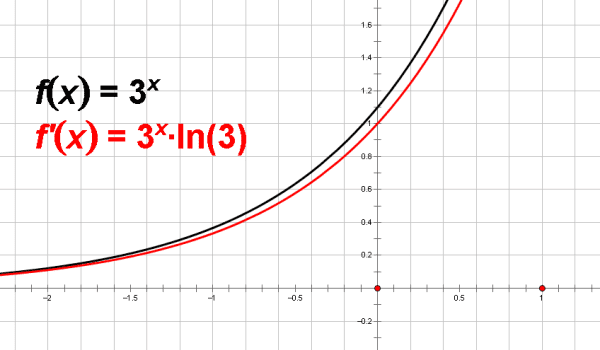
如有不懂,欢迎继续追问,随时为您解答。
y=(3x-2)/(2x^2-3x+1)的n阶导数
【用归纳的方法】
y=3^x
一阶导数y'(1)=3^x*ln3
二阶导数y'(2)=3^x*(ln3)²
三阶导数y'(3)=3^x*(ln3)³
···
n阶导数y'(n)=3^x*(ln3)^n
~手机提问者在客户端上评价点【满意】即可~~
~您的采纳是我前进的动力~~
~如还有问题,可以追问~~
~祝学习进步,更上一层楼!O(∩_∩)O~
3的x次方的导数
[(sinx)^3]'=3(sinx)^2 *cosx。[sin x^3]'=3x^2 *cosx^3。
分析过程如下:
如果是(sinx)^3,那么求导得到:3(sinx)^2 *cosx。把(sinx)^3看成一个复合函数,u=sinx,y=u^3。
而如果是sin x^3,那么求导就得到:cosx^3 *(x^3)' 即3x^2 *cosx^3。把sin x^3看成一个复合函数,u=x^3,y=sinu。
扩展资料:
链式法则:若h(a)=f[g(x)],则h'(a)=f’[g(x)]g’(x)。
链式法则用文字描述,就是“由两个函数凑起来的复合函数,其导数等于里函数代入外函数的值之导数,乘以里边函数的导数。”
常用导数公式:
1.y=c(c为常数) y'=0
2.y=x^n y'=nx^(n-1)
3.y=a^x y'=a^xlna,y=e^x y'=e^x
4.y=logax y'=logae/x,y=lnx y'=1/x
5.y=sinx y'=cosx
6.y=cosx y'=-sinx
7.y=tanx y'=1/cos^2x
8.y=cotx y'=-1/sin^2x
9.y=arcsinx y'=1/√1-x^2
10.y=arccosx y'=-1/√1-x^2
以上就是关于3的x次方的导数怎么,三的x次方的导数是多少的全部内容,以及3的x次方的导数怎么求的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。





