初中数学方差怎么求
设一组数据x1,x2,x3……xn中,各组数据与它们的平均数x(拔)的差的平方分别是(x1-x拔)2,(x2-x拔)2……(xn-x拔)2,那么我们用他们的平均数来衡量这组数据的波动大小,并把它叫做这组数据的方差。
方差公式是一个数学公式,是数学统计学中的重要公式,应用于生活中各种事情,方差越小,代表这组数据越稳定,方差越大,代表这组数据越不稳定。若x1,x2,x3......xn的平均数为m则方差
例1两人的5次测验成绩如下:
X:50,100,100,60,50E(X)=72。
Y:73,70,75,72,70E(Y)=72。
平均成绩相同,但X不稳定,对平均值的偏离大。方差描述随机变量对于数学期望的偏离程度。
初中课本上的方差的计算公式有错误
方差公式:
若x1,x2,x3......xn的平均数为m,则方差s^2=1/n[(x1-m)^2+(x2-m)^2+.......+(xn-m)^2]
方差即偏离平方的均值,称为标准差或均方差,方差描述波动程度。
方差是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望(即均值)之间的偏离程度。
统计中的方差(样本方差)是每个样本值与全体样本值的平均数之差的平方值的平均数。在许多实际问题中,研究方差即偏离程度有着重要意义。
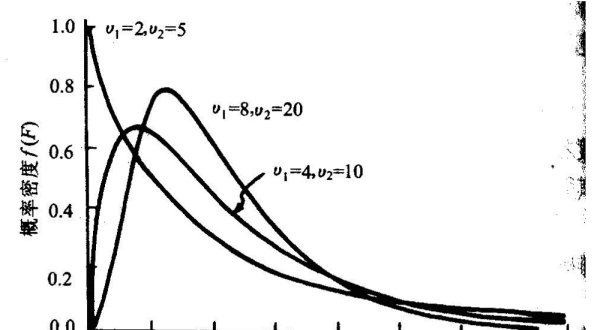
方差的统计学意义
当数据分布比较分散(即数据在平均数附近波动较大)时,各个数据与平均数的差的平方和较大,方差就较大;当数据分布比较集中时,各个数据与平均数的差的平方和较小。因此方差越大,数据的波动越大;方差越小,数据的波动就越小。
样本中各数据与样本平均数的差的平方和的平均数叫做样本方差;样本方差的算术平方根叫做样本标准差。样本方差和样本标准差都是衡量一个样本波动大小的量,样本方差或样本标准差越大,样本数据的波动就越大。
初中数学方差公式例题
①若x1,x2....xn 的平均数为m,
其方差是:S^2=1/n[(x1-m)^2+(x2-m)^2+.......+(xn-m)^2]
标准差:S=√{1/n[(x1-m)^2+(x2-m)^2+.......+(xn-m)^2]}
②若x1,x2....xn 其方差是:S²
则kx1,kx2.....kxn的方差为:k²S²
③ 若x1,x2....xn 其方差是:S²
则x1+a,x2+a,x3+a....xn+a的方差为:S²(没有改变)
(k1,a是不为零的常数)
④若x1,x2....xn 其方差是:S²
则kx1+a,kx2+a,kx3+a....kxn+a的方差为:k²S²
初中方差的计算公式
初中方差的计算公式是S^2=1/n[(x1-x)^2+(x2-x)^2+……+(xn-x)^2]。
方差是和中心偏离的程度,用来衡量一批数据的波动大小(即这批数据偏离平均数的大小)并把它叫做这组数据的方差,记作S^2。在样本容量相同的情况下,方差越大,说明数据的波动越大,越不稳定。计算公式为:S^2=1/n[(x1-x)^2+(x2-x)^2+……+(xn-x)^2]。
其中:x为这组数据中的数据,n为大于0的整数。
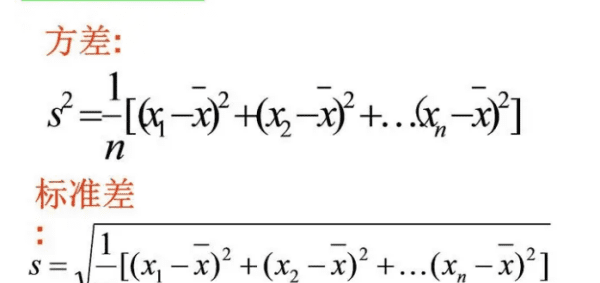
方差的定义和性质:
1、方差是一组数据中每个值与数据平均数之差的平方的平均数,在概率论中用来度量随机变量和其均值之间的`偏离程度,在统计学中是一组数据时离散程度的度量。
2、极差,又称范围误差或全距,用字母R表示,是用来表示统计资料中的变异量数,通过最大值减最小值后得出数据,通常用来反映一组数据变化范围的大小。极差不能用作比较,因为数据的单位不同,方差能用作比较,因为都是个比率。
方差公式初中数学
方差的计算公式为:方差=(各个数据与平均数之差的平方的和)÷(数据个数-1)。
1.方差的概念
方差是用来衡量一组数据的离散程度,它反映了数据集中的每个数据点与数据集的平均值之间的偏离程度。方差越大,数据点越分散;方差越小,数据点越集中。

2.方差的计算步骤
计算一组数据的方差可以通过以下步骤实现计算数据的平均值,即将所有数据相加,然后除以数据个数,得到平均值。计算每个数据点与平均值的差值,即将每个数据减去平均值。将每个差值平方,得到每个数据点与平均值之间的偏离程度的平方。计算所有偏离程度的平方的和,并除以数据个数,得到方差。
3.方差的计算公式
在数学中,方差的计算有两种常见的公式样本方差的计算公式:样本方差=Σ(x-x̄)²/(n-1)其中,xi表示每个数据点,x̄表示数据的平均值,n表示数据个数。总体方差的计算公式:总体方差=Σ(xi-x̄)²/n其中,xi表示每个数据点,x̄表示数据的平均值,n表示数据个数。
4.方差的应用举例
方差在实际生活和统计学中有着广泛的应用。例如:在股票市场中,用方差来衡量投资组合的风险。方差越大,代表投资组合的风险越高。在质量控制中,用方差来衡量产品的稳定性和一致性。方差越小,代表产品的质量越稳定。在社会调查中,用方差来衡量样本数据的离散程度。方差越大,代表样本数据的分布越分散。

总结:
方差是用于衡量一组数据的离散程度的统计量。初中数学中,方差的计算可以通过一定的步骤和公式来实现,包括样本方差和总体方差两种计算方式。方差在实际生活和统计学中有着广泛的应用,它可以帮助我们理解数据的分布和变异情况,为决策和分析提供有力的支持。
以上就是关于初中数学方差怎么,初中课本上的方差的计算公式有错误的全部内容,以及初中数学方差怎么求的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。