空间向量在坐标轴上的投影怎么求
空间向量在坐标轴上的投影求法:一个向量在另一个向量上的投影既不是向量也不是长度,而是一个实数,其绝对值是长度。公式是a在b上的投影=a*b/|b|。
空间中具有大小和方向的量叫做空间向量。向量的大小叫做向量的长度或模。规定,长度为0的向量叫做零向量,记为0。模为1的向量称为单位向量。与向量a长度相等而方向相反的向量,称为a的相反向量。记为-a方向相等且模相等的向量称为相等向量。
空间向量的投影向量怎么求
对于求向量在另一个的投影,首先你需要求出夹角(或者夹角正玹值),然后把需要求的向量乘以夹角的余玹值即可。
如a在b上的投影是|a|cos
=a*b/|b|
a=(1,2,3)
b=(2,1,4)
a在b上的投影为:
a*b=2+2+12=16
|b|=√(2^2+1^2+4^2)=√21
a在b上的投影为:
16/√21
空间向量的投影向量坐标怎么求
投影向量的坐标怎么求介绍如下:
投影向量的坐标求法是一种计算投影向量的坐标的方法。它的基本思想是:给定一个向量A,求另一个向量B在A上的投影,即求B在A上的投影向量。首先,计算A和B的内积,即A·B,然后计算A的模,即|A|,最后将A·B除以|A|,得到投影向量的模,即|P|。
接下来,计算投影向量的方向,即A/|A|,将其乘以|P|,得到投影向量的坐标,即P=(A/|A|)*|P|。最后,将投影向量的坐标代入到向量的坐标表达式中,即P=(x,y,z),即可求出投影向量的坐标。
投影向量定义是什么?
比如ab (a,b是向量)
ab=|a||b|cos
a在b上的投影就是|a|cos
同理,b在a上的投影就是|b|cos
令投射线通过点或其他物体,向选定的投影面投射,并在该面上得到图形的方法称为投影法。
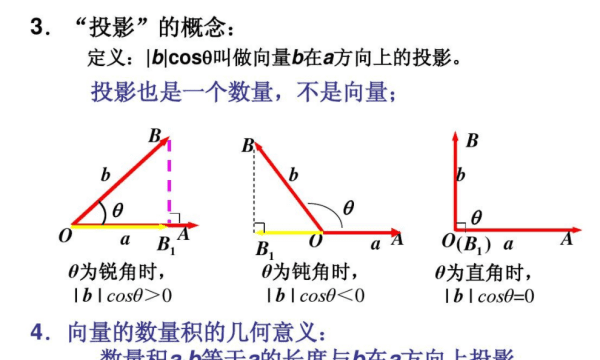
设两个非零向量a与b的夹角为θ,则将|b|·cosθ 叫做向量b在向量a方向上的投影或称标投影。
相关内容介绍:
一个向量在另一个向量方向上的投影是一个数量。当θ为锐角时,它是正值;当θ为直角时,它是0;当θ为钝角时,它是负值;当θ=0°时,它等于|b|;当θ=180°时,它等于-|b|。
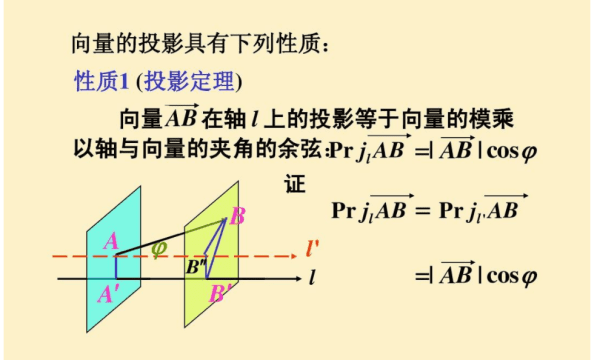
设单位向量e是直线m的方向向量,向量AB=a,作点A在直线m上的射影A',作点B在直线m上的射影B',则向量A'B' 叫做AB在直线m上或在向量e方向上的正射影,简称射影。
向量A'B' 的模 |A'B'|=|AB|·|cos〈a,e〉|=|a·e|。
行列式的值是一个数字,表示向量所在空间的【元素】 大小。
比如,在平面直角坐标系中,整个平面可以由长宽均为1的方格构成,这个方格的大小为1。这个方格就是平面直角坐标系中的【元素】,大小为1。
因为方向不能比较大小,所以向量也就不能比较大小。对于向量来说“大于”和“小于”的概念是没有意义的。
当用有向线段表示向量时,起点可以任意选取。任意两个相等的非零向量,都可用同一条有向线段来表示,并且与有向线段的起点无关.同向且等长的有向线段都表示同一向量。
一个向量在x轴的投影等于
向量(a,b)=(a,0)+(0,b);
上述(a,0)就是它在x轴上的投影;(0,b)是在y轴上的投影。
【要注意一点是,投影也是一个向量】
求法是:把向量(a,b)的起点移到原点处,则它的终点坐标就是(a,b),于是它在x轴上投影横坐标是a,投影就是(a,0),在y轴上投影纵坐标是b,投影就是(0,b)。
空间中向量在坐标轴上的投影
一个向量在另一个向量上的投影既不是向量也不是长度,而是一个实数,其绝对值是长度。
公式:a 在 b 上的投影 = a*b / |b| 。
以上就是关于空间向量的投影向量怎么求,空间向量在坐标轴上的投影怎么的全部内容,以及空间向量在坐标轴上的投影怎么求的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。