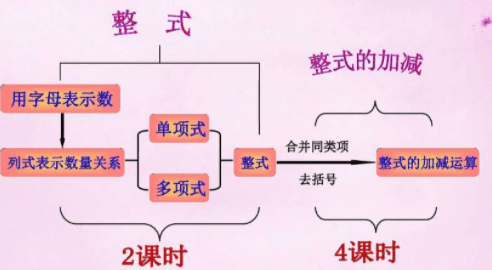
整式的加减的实质是什么
整式的加减运算实质就是合并同类项。
整式是有理式的一部分,在有理式中可以包含加,减,乘,除四种运算,但在整式中除数不能含有字母。
单项式和多项式都统称为整式。
把一个多项式化为几个最简整式的乘积的形式,这种变形叫做把这个多项式因式分解(也叫作分解因式)。
分解因式与整式乘法为相反变形。
整式的加减知识点总结归纳
整式的加减实质上就是去括号,合并同类项,结果总是比原来简洁,体现了数学的简洁美。
整式的加减是七年级的,整式为单项式和多项式的统称,是有理式的一部分,在有理式中可以包含加,减,乘,除、乘方五种运算,但在整式中除数不能含有字母。
易错混点:
(1)多项式的次数是次数最高项的次数,而不是各项次数的和,应理解透概念。
(2)看清是降幂还是升幂排列。
(3)降幂和升幂排列都是以某一个字母(未知量)来排序。
加减法的性质:
从加法交换律和结合律可以得到:几个加数相加,可以任意交换加数的位置;或者先把几个加数相加再和其他的加数相加,它们的和不变。
几个数的和减去一个数,可以选其中任一个加数减去这个数,再同其余的加数相加。例如:(35+17+29)-25=35-25+17+29=56。
整式的加减运算实质上是什么
整式的加减运算实质就是合并同类型。
整式的加减实质上就是什么和什么的综合运用
一、常考知识点
1 、整式的概念
整式:(i)多项式 多项式的次数 项数 系数 升降幂排列;(ii)单项式 单项式的次数 系数
整式
(1)整式中只含有一项的是单项式,否则是多项式,单独的字母或常数是单项式;
(2)单项式的次数是所有字母的指数之和;
多项式的次数是多项式中最高次项的次数;
(3)单项式的系数,多项式中的每一项的系数均包括它前面的符号
(4)同类项概念的两个相同与两个无关:
两个相同:一是所含字母相同,二是相同字母的指数相同;
两个无关:一是与系数的大小无关,二是与字母的顺序无关;
(5)整式加减的实质是合并同类项;
(6)因式分解与整式乘法的过程恰为相反。
2、整式的运算
3、因式分解
4、分式的概念
(1)分式的定义:整式A 除以整式B,可以表示成B/A的形式。如果除式B 中含有字母,那么称B/A为分式,其中A 称为分式的分子,B 为分式的分母。对于任意一个分式,分母都不能为零。
(2)分式的约分
(3)分式的通分
5、分式的性质
6、根式的有关概念
7、二次根式的性质
8、二次根式的运算
(1)二次根式的加减
二次根式相加减,先把各个二次根式化成最简二次根式,再把同类二次根式分别合并。
(2)二次根式的乘法
二次根式相乘,等于各个因式的被开方数的积的算术平方根,即二次根式的和相乘,可参照多项式的乘法进行。
两个含有二次根式的代数式相乘,如果它们的积不含有二次根式,那么这两个二次根式互为有理化因式。
(3)二次根式的除法
二次根式相除,通常先写成分式的形式,然后分子、分母都乘以分母的有理化因式,把分母的根号化去(或分子、分母约分).把分母的根号化去,叫做分母有理化。
整式的加减运算实质就是
整式的加减运算实质就是合并同类项,
以上就是关于整式的加减的实质是什么,整式的加减知识点总结归纳的全部内容,以及整式的加减的实质是什么的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。