奇函数f0一定等于0吗?
不一定。若f(x)为奇函数,且在x=0处有意义,则f(0)=0。奇函数是指对于一个定义域关于原点对称的函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)就叫做奇函数。
f(0)=0是否为奇函数
f(0)=0,不一定是奇函数,如:f(x)=x2,满足f(0)=0,但这明显是个偶函数。
奇函数也不一定有f(0)=0,如:f(x)=1/x,这是一三象限的反比例函数,关于原点对称,是奇函数,但明显没有f(0)=0这一结论。
正确的说法是这样的:对于奇函数而言,若0属于定义域,则必有f(0)=0。
若f(0)≠0,则必有0不属于定义域。
奇函数一定为f(0)=0吗
奇函数从函数关系式上看要满足f(-x)=-f(x),当x=0时,推导出f(-0)=-f(0),即f(0)=0,从函数图象上看,图象是关于原点(0,0)对称的。
所有奇函数都有f0等于零吗
不一定。
因为 f(-x)=-f(x),将x=0代入,得f(0)=-f(0),从而f(0)=0。
奇函数特点介绍:
1、奇函数图象关于原点(0,0)对称。
2、奇函数的定义域必须关于原点(0,0)对称,否则不能成为奇函数。
3、若 f(x)为奇函数,且在x=0处有意义。
4、设 f(x)在定义域I 上可导,若f(x)在I上为奇函数,则f'(x)在 I上为偶函数。
即f(-x)= - f(x)对其求导f'(x)=[-f(-x)]'(-x)'=-f'(-x)(-1)=f'(-x)。

奇函数的性质:
1、两个奇函数相加所得的和或相减所得的差为奇函数 。
2、一个偶函数与一个奇函数相加所得的和或相减所得的差为非奇非偶函数。
3、两个奇函数相乘所得的积或相除所得的商为偶函数。
4、一个偶函数与一个奇函数相乘所得的积或相除所得的商为奇函数。
5、当且仅当 (定义域关于原点对称)时, 既是奇函数又是偶函数。奇函数在对称区间上的积分为零。
奇函数f0一定等于0条件
不一定,
如果X∈R,
则f(0)=0
若X≠0
则f(0)不存在:
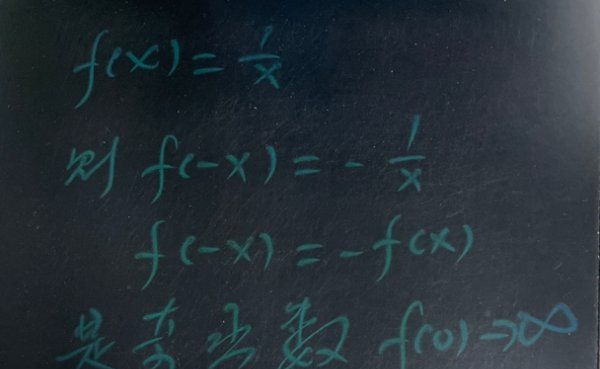
上图f(0)不存在
f0=0一定是奇函数吗
不一定,f(0)=0只是奇函数的一个性质,要判断函数的奇偶性要靠定义,首先定义域关于原点对称,然后图像关于原点对称
奇函数f0都等于0吗
不一定,奇函数还可能在x=0这一点无定义。例如f(x)=1/x这个函数就是奇函数,但是这个函数在x=0这点无定义。
但是如果一个奇函数在x=0这点有定义,那么f(0)必然等于0
因为根据奇函数的定义,当f(0)有定义时,f(0)=-f(0)
所以f(0)=0
以上就是关于奇函数f0一定等于0,所有奇函数都有f0等于零吗的全部内容,以及奇函数f0一定等于0吗?的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。





