复利计算公式解释
1、复利终值,也叫按复利计算的本利和。复利终值=本金+利息,提取公因子得:复利终值=本金×(1+利率)N(注:此处的N为N次幂,表示期数。)
2、复利现值,是知道本利和求本金,是上面公式基础变形:复利现值(本金)=复利终值/(1+利率)N(注:此处的N为N次幂,表示期数。)
复利的计算公式
复利的计算公式为:F=P*(1+i)^n。

复利是指一笔资金除本金产生利息外,在下一个计息周期内,以前各计息周期内产生的利息也计算利息的计息方法。复利的计算是对本金及其产生的利息一并计算,也就是利上有利。复利计算的特点是:把上期末的本利和作为下一期的本金,在计算时每一期本金的数额是不同的。
复利现值是指在计算复利的情况下,要达到未来某一特定的资金金额,现今必须投入的本金。 所谓复利也称利上加利,是指一笔存款或者投资获得回报之后,再连本带利进行新一轮投资的方法。简单来讲,就是在期初存入A,以i为利率,存n期后的本金与利息之和。公式:F=A*(1+i)^n。
例如:本金为50000元,利率或者投资回报率为3%,投资年限为30年,那么,30年后所获得的利息收入,按复利计算公式来计算本利和(终值)是:50000×(1+3%)^30。
由于,通胀率和利率密切关联,就像是一个硬币的正反两面,所以,复利终值的计算公式也可以用以计算某一特定资金在不同年份的实际价值。只需将公式中的利率换成通胀率即可。

复利的应用:
复利终值:商务印书馆《英汉证券投资词典》解释:复利 compound rate;compound interest;interest on interest。由本金和前一个利息期内应记利息共同产生的利息。即由未支取利息按照本金的利率赚取的新利息,常称息上息、利滚利,不仅本金产生利息,利息也产生利息。
普通年金终值:指一定时期内,每期期末等额收入或支出的本利和,也就是将每一期的金额,按复利换算到最后一期期末的终值,然后加总,就是该年金终值。
例如:每年存款1元,年利率为10%,经过5年,逐年的终值和年金终值,公式为:F=A[(1+i)^n-1]/i,记作F=A(F/A,i,n)。
复利的公式
复利的计算公式为:S=P×(I+i)^n,其中I代表利息;P代表本金;n代表期数;i代表利率;S代表复利计算出的本利和。复利是指在计算利息时,某一计息周期的利息是由本金加上先前周期所积累利息总额来计算的计息方式,常用于对本金及其产生利息的计算。

其次,我们还是需要明白,与复利相对的就是单利。单利就是不会把我们的利息算作本息,简单来讲,就是每年的息都是一样的,这里的一样是指我们的本金没有发生变化作为前提下一样。而复利就是利滚利。我们需要明白这两者的区别。
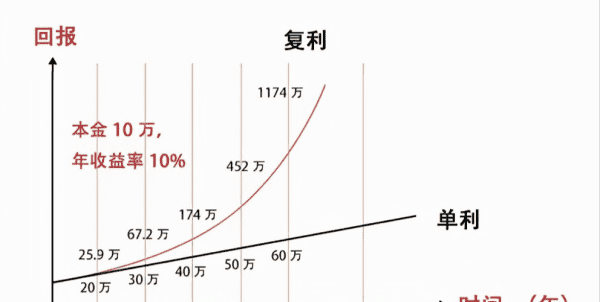
复利的计算公式是什么样的?
复利的计算是考虑前一期利息再生利息的问题,要计入本金重复计息,即“利生利”“利滚利”。
计算公式及定义如下:
F=P*(1+i)^n
F=A((1+i)^n-1)/i
P=F/(1+i)^n
P=A((1+i)^n-1)/(i(1+i)^n)
A=Fi/((1+i)^n-1)
A=P(i(1+i)^n)/((1+i)^n-1)
F:终值(Future Value),或叫未来值,即期末本利和的价值。
P:现值(Present Value),或叫期初金额。
A :年金(Annuity),或叫等额值。
i:利率或折现率
N:计息期数
主要分为2类:一种是一次支付复利计算:本利和等于本金乘以(1+i)的n次方,公式即F=P(1+i )^n;
另一种是等额多次支付复利计算:本利和等于本金乘以(1+i)的n次方-1的差后再除以利息i,公式即F=A((1+i)^n-1)/i
以上就是关于复利的计算公式,复利计算公式解释的全部内容,以及复利计算公式解释的相关内容,希望能够帮到您。
版权声明:本文来自用户投稿,不代表【易百科】立场,本平台所发表的文章、图片属于原权利人所有,因客观原因,或会存在不当使用的情况,非恶意侵犯原权利人相关权益,敬请相关权利人谅解并与我们联系(邮箱:350149276@qq.com)我们将及时处理,共同维护良好的网络创作环境。